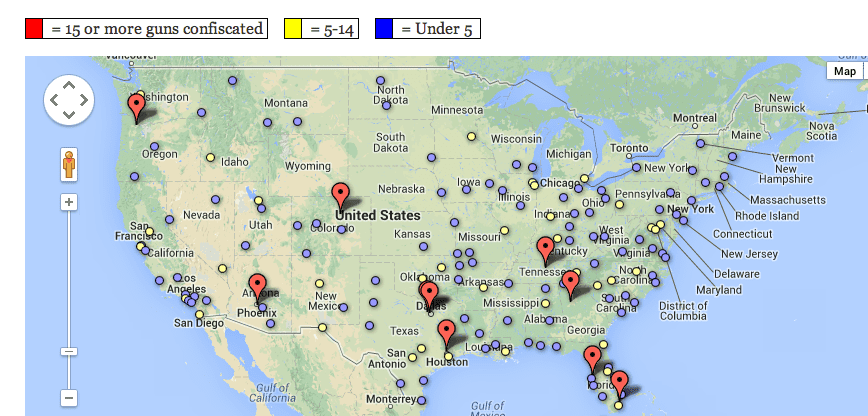
“Another arrest has put Orlando International in the lead for the number of guns seized at Florida airports, perhaps boosting police hopes for signs warning OIA travelers against bringing loaded weapons into the terminal,” orlandosentinel.com reports. “A loaded pistol confiscated Thursday from a Texan broke Orlando’s tie with Tampa International Airport for statewide bragging, or blushing, rights, for a total of 29 handguns so far this year.” That still puts Orlando one behind Salt Lake City, who found their 30th gun last Tuesday, packed in the carryon of a man going to Vegas, baby! Speaking of Lone Star take downs, you may recall the TSA’s Blue Shirted goons’ arrested Ted Nugent’s wife Shemane Deziel on a similar charge on the 29th. That would be firearm number 701 for the year or thereabouts, as nationalsecurityzone.org reveals. [Map above shows TSA gun grabs by airport for the same period in 2012.] We don’t know how many inadvertent (if ignorant) gun schleppers the TSA arrested but . . .
we do know how many of them were charged under terrorism statutes. None. Not one.
So here’s an idea: if someone mistakenly brings a gun to an airport security checkpoint and it’s detected (not a given), make sure the offending passenger isn’t a bad guy, tell them to cut that sh*t out, then let them ship the gun home. Wish them a safe flight (if they haven’t missed it) and leave it at that.




Yeah, but then they don’t get to be heros.
“So here’s an idea: if someone mistakenly brings a gun to an airport security checkpoint and it’s detected (not a given), make sure the offending passenger isn’t a bad guy, tell them to cut that sh*t out, then let them ship the gun home. Wish them a safe flight (if they haven’t missed it) and leave it at that.”
Your argument is dictated by the soundest of reason. Thus, TSA will summarily ignore it.
Yes, after all, we are talking about the same folks who think that guns go off when you toss them through and x-ray machine……
I think we are missing an important point here. It is not TSA who arrest the absent minded passengers, but the local P.D. on each jurisdiction. All TSA does is stopping the boarding process and handling you over to the police. Key point: Don’t try to board a plane while carrying. Once you put your EDC bag with your gat on their conveyor belt or walk into their body scanners with your gun on your hip and THEY discover it, you are pretty much done. If you remember at the very last second before being scanned; dont say anything, turn and walk away from the checkpoint and fix the issue before they have to tell you.
I’ve donated a few small pocket knives to TSA agents when I realized I had one in a pants pocket while going through them before the xray belt area. One knife I was able to get back to the gate and they actually went and put it in my checked bag (which rocked!), but normally I walk up to the closest person (away from the metal detectors) and apologize and say I didn’t realize it was in my pocket and they tell me no problem, toss it in the trash. At which point I ask if they will just take it and keep it for themselves or give it to someone who would like it, etc. A shame to waste it. Most have said okay and taken it 😉
Once you step into the area, you can be searched, if I remember correctly. At least from the signs at the airport. It’s up to the TSA agent to let you go, but “Yeah, I forgot to leave my CCW out” is probably not going to get a happy response.
So sorry, my friend, but merely releasing such obvious evil-doers with just a warning would not provide the absolutely-necessary ‘Security’ Kabuki Theatre so necessary to the continued survival of TSA. Beyond the occasional discovered firearm, every single day, without fail, TSA successfully protects us from breast milk, water, toothpaste, cosmetics, shoes, very small children, the elderly, the disabled, wounded veterans, food, and other Terrors of the Skies too numerous to mention.
We should applaud our TSA as the steadfast and ever-vigilant warriors that they are, and not belittle them when they merely do their duty.
I think I just threw up a little in my mouth.
Kabuki theater was on display when my toddler’s diaper bag was rummaged through. You would have thought they found the holy grail or a stick of dynamite after a partially empty baby sunscreen lotion container was discovered. It didn’t help that at the same time they found a micro sized multitool in my wife’s purse. Oh lord we are going to take a plane with a 1 inch knife on a multitool. At least we made it to the gate in time.
I am so goddamn furious about the reversal of the reversal on small pocketknives because of the sky waitresses case of the vapors…
A good friend of mine several years ago went through “security” with a handful of fireworks in his pocket… Was an early New Years day flight and he’d wanted to shoot them off the night before, then ended up drinking a bit much, got a ride home, slept in his clothes, and got a ride to the airport… He realized after going through and reaching into his pocket, discretely dumped into a trash can…
What about all of the people who mistakenly (or not, I suppose) get through security with their firearm (loaded, with one in the chamber even) and absolutely NOTHING happens?
They could be LEOs or Sky Marshals. Or not…
It seems to me that the most effective means to stop a high jacking is to arm everyone who gets on the plane. This would virtually ensure that any high jacker(s) would be out numbered and outgunned by the passengers. Given the events of 9/11 I’m doubting that there are many not willing to fight to prevent high jackers from taking the plane they’re on. Then we could simply recover the weapons issued at the other end of the flight (for those who didn’t bring their own) and reissue them on an outbound flight. No more need for the TSA, stripping, being semi-molested and having our shampoo stolen. No more need for air marshals, and absolutely positively no more 9/11’s. Cheap, convenient and effective, no way it will ever be implemented.
everyone is a bit much. 10% would be more than sufficient. furthermore, unless the cockpit is bulletproof, the terrorists could simply shoot through the wall and kill the pilot. mission accomplished.
A shiv in every barf bag? While I don’t think the majority of people are nut jobs that will stab you in the throat over a bag of peanuts, the antis are starting to convince me there are more than I thought. I don’t think you should hand a weapon to some that wasn’t confident or competent enough to have one in the first place.
In the months before 9/11 I was on a flight where I had no less than 5 knives between 2-5″ in my carry on. (In condition white, I didn’t even know what EDC meant back then) They passed through the X-ray with out anyone batting an eyelash. Best part, The plane didn’t crash.
I like the idea of armed passengers on a plane with a couple of tweaks. Holsters must meet certain criteria( completely cover the trigger gaurd, etc.) and all airport bars and inflight alcohol service done away with.
I have advocated for years; fly naked or armed. Unless your willing to hide a weapon in a very personal spot, a firearm to any one willing to bring it on the flight is common sense.
Agree to disagree. The Captain has the ultimate say on who rides his plane and who doesn’t. Once you push back from the gate, passengers in the seats are no longer the masters of their domain, and the responsibility for their safety has been assumed by the Captain.
CCW on an aircraft are not a good idea, mostly because planes don’t play nice when complex and relatively delicate systems get holes punched in them.
“Know your target and what’s behind it” kind of goes right out the window when you unload on johnny jihawd at FL370.
All the more reason to support people like me carrying on aircraft. My reason are:
1.) Retired military aircraft maintenance technician, with a GREAT deal of knowledge as to what NOT TO SHOOT. Small Arms Expert rifle/pistol/revolver/shotgun.
2.) Top Secret/Nuclear security clearance(s) for 20 years.
3.) 12 1/2 years as an Air Force Security Policeman as an additional duty. Qualified as a “designated marksman”.
4.) Weapons trainer for Base Honor Guard (several different assignments/bases)
5.) Experience on 2 civilian police forces.
6.) NRA certified Firearms Instructor.
7.) Well qualified in close-quarter hand-to-hand fighting.
8.) Will work for FREE.
You’d really only need for the female flight attendants to be naked. I understand that Islam has some kind of rule that if you see a naked woman, it’s some kind of sin and you won’t get to go to heaven and get the 72 Virginians. So they wouldn’t even get on the planes.
Serve only pork in the terminals within or heading to the US, bacon everything including the water. The TSA agents lube their gloves up with pig fat. Require all passengers to pop a pork pill as they go through security. A special aerosol pork spray that shoots in your mouth before the x-ray. Lets see anybody think they’re gonna see their 72 virgins after that. Maybe just have a constant cloud of the smell of cooking bacon cover the entire country?
Like that crazy guy said in Robocop when he fired that freakin’ hand-held cannon, I LIKE it!
And put up public notices: WARNING! THE REMAINS OF ANY TERRORIST KILLED BY THEIR OWN SUICIDE BOMBS WILL BE STERILIZED BY BOILING IN LARD AND FED TO LIVE HOGS! Plus the translations to Arabic and (just to be on the safe side) Farsi.
Kinda reminds me of Scott Adams’ proposal for “Atheist Airlines.” I paraphrase here:
Instead of a security gate with x-rays and body cavity probes and schtuff, you have a booth with at least one icon from each religion, and have passengers come in and blaspheme all the gods. Then let them carry chainsaws, bazookas, whatever they want onto the airplane. He remarks something to the effect that Atheists generally don’t go around starting trouble unless there’s a handy means of escape nearby. (which an airplane in flight doesn’t really have.)
Some years ago I saw a political cartoon captioned “If we really lived in a free society.” The cartoon is the inside of the airplane with a couple of arab-lookng guys with utility knives surrounded by about 6 or 8 people all with their CC pieces out, and the hijackers in their sights. One of the hijackers says, “Uh, we just wanted to see if the pilot had any boxes he needed opened….”
I don’t see how it’s any different than a 4oz shampoo bottle. You should have the option to drop it in the TSA’s fringe benefits bin, or mail it to yourself before boarding.
But seriously, how do you forget you have a gun on you?
It easy Layne. I have carried for over forty years. If I am dressed I have my concealed weapon on me. Not any differnt than forgetting you have change in your pocket. Just forget its there. Walked into many banks and realized I am armed. Not supposed to do that but shit happens.
Sure, but walking into a bank is an everyday activity. Getting on a plane, not so much. For the vast majority of people, flying somewhere is a somewhat rare occurrence, so the “I forgot I had a gun” defense is pretty weak. I mean, in the hours between packing their bags, driving to the airport, checking their bags, checking in at the airline desk, and walking to the security checkpoint, these people had zero thoughts about their gun? That must be a freakin’ comfortable holster!
In an age when you can’t take nail clippers on a plane, there’s no excuse beyond “superhuman stupidity” for getting stopped at the genital-fondling-and-irradiation station with a gun.
Folks TSA doesnt make the arrest. And they dont (Confiscate) the firearm. TSA does exactly what the post above requests. Find it, inform the passenger that its not allowed give them the option to check it or do something else with it. They also notify a local LEO. ANY arrest made is after the fact, and is done by the local LEO, for a violation of local laws or airport regulations.
Also, hands of my balls.
Really? I pay extra for that sort of service.
TSA: Is that a liberator or are you just glad to see me?
Me: You can’t tell by the smile on my face? 🙁
I had tried to bring a brand new, still in original blister packing, obviously empty Kimber magazine in my briefcase as a gift to my son who I was traveling to see. It took a team of 3 TSA folks about 10 minutes to render their verdict that no I could not carry that onto a plane. Explain to me how that was a danger to anyone? I am a frequent flyer so two of the TSA folks know me by name. They did let me get out of line and take it to my car (small airport thankfully) but it just seemed so overboard….
Silly man. . . you could’ve met up with the guy who had already smuggled the slide, frame, innards, and ammunition onto the aircraft–and then, with YOUR MAGAZINE to complete the gun, you or he could’ve killed everyone aboard along with their puppies.
You were lucky not to be shot. /sarc
TSA doesn’t arrest people. Local LE does. Nice story TTAG.
As if detaining you with force of law for the police to come collect you is effectively any different.
TSA is so lax with their scanning, I’ve gotten a number of things through their scanners that I shouldn’t have numerous times.
I once brought a bottle of some sort of liquid to the checkpoint. This was in the early days of the recent TSA insanity. They told me I couldn’t have it on the plane and tossed it in a trash can behind them. All I could think was that if they thought it was so dangerous and explosive, why did they allow it to sit in a can two feet behind them? And if they trusted it with their lives, why couldn’t I have it back?
Sir I agree with you, but mostly its a matter of the people making the decisions not being the ones who have to deal with the consequences, and considering the TSO’s to be expendable. There are not enough resources to test every single thing that comes through, so they cant let it go, but they have to something with it. At my airport you cant take it with you but, if its new and unopened, you can donate it to the USO, who give it to active duty military who come through the airport. I dont know who looked at that and said new and unopened was safe enough to give to the USO, but not safe enough to fly.
Somehow, I doubt the guys who flip out over nail clippers and toothpaste would react well to something as suspicious as common sense.
yeah, TSA has no arrest powers and cannot arrest anyone. i know bashing them is VERY popular, but maybe we should bash them for what they actually do?
So who calls the police when things like this go down?
Yeah, the TSA deserves all the bashing they get.
The Federal government would never let them go scot free. That would make their War on the American people silly now, wouldn’t it?
Idea for TSA how about they just charge the individual a small fee an have a licensed FFL send the gun home. Second all unless I’m carrying concealed my weapon I maintain a unloaded weapon when transporting it anywhere. Most of these individuals need to understand that you should check your stuff before heading out to the airport. A lot of issues can be avoided by doing a simple sanity check.
All the comments I read acted like “those poor people! TSA shame on you!” But last I checked (I carry whenever I am dressed and even when not dressed, my weapon is not far away) it would be ignorant, or at least DUMB to forget you have a weapon on your person… it isn’t the TSA’s fault you FORGOT! We all know you can’t bring a weapon on a plane… if you are stupid, you pay….no?
Don’t bring a loaded or unloaded gun with you through the TSA check-point. Frak…simple as that. If you forgot that you have a firearm on while you are in line about to be X-rayed…that is your own fault or should not even be owning a gun. Because if you forget that it is on you, who knows what else you might have forgotten with any firearm. Isn’t that one of the rules of gun safety. Everyone knows this. If you feel you need to bring a firearm on a plane…take another form of transportation. If you do not like the rules please drive, take a bus, a train, a boat, or whatever else. There are options. For those who hunt overseas, re-read the TTAG’s article on that. This is common sense that makes the rest of us look like idiots.
Seems like a new business opportunity. Open a business inside the airport BEFORE the secure area. Pre-TSA Scan. Rent scanners and hire off-duty TSA agents.
Scan you and your bags for a reasonable fee. If something is found, you have time to correct it before entering the secure area.
I’m sorry but I beg to disagree. You try to bring a gun on board, you should pay the price for your forgetfulness, malice, or idiocy. “Special consideration” smacks of something the libs would come up with
GUNS ARE NOT AN ACCESSORY.
I think a lots of folks (from the descriptions) have a gun stuffed in a purse or briefcase and forget they are there. They deserve (Imho) to have their guns confiscated because they are a danger to themselves& others. They got the ‘where not to carry’ if they have a carry permit. The others (and it feels like half) don’t have a permit and that’s a felony, period.
Also, low penalties let the enemy test and fail without penalty. A bad idea.
I’d bet the same % of idiots get caught at our courthouses, but there’s fewer so it’s not as newsworthy.
I’d vote we create an additional civilian carry with near Leo requirements for weapons training and let them be ‘first responders’ with allowed carry ANYWHERE.
Why hasn’t a Major Airline stepped up and created flights for passengers that have CHL’s? This would create FREE Airport Security. FREE Airline Security. No need to have TSA Security stations because all passengers would be armed. Terrorist would stay away and frequent some other country that doesn’t allow it’s citizens to be armed.
Der Fuehrer is far too terrified to let that happen.
Why bash the TSA agents ? Seems to me they are just men and women that needed a job and are following the rules that the higher ups at TSA have given them. Most I have dealt with are pretty easy to get along with. Always a few exceptions but that is true with any group. I typically check my weapon along with my bags. Requires dealing with a TSA agent but they have always been cordial and polite with me. I suspect that if they give anyone too much leeway they might lose their jobs. I also suspect that their jobs are not all the great and they may have trouble finding another job if they lose the one they have. They are just people. If anyone has a beef with the TSA it should be with the folks higher up the ladder that make the rules not the agents on the line enforcing them.
Comments are closed.