1. The North Carolina Council of Churches plans to put up a billboard on a local interstate in the coming days, and it expects the sign to attract some attention.

   The message? That the Second Commandment – that no idol shall be worshiped – supersedes the Second Amendment that gives citizens the right to bear arms.

   The billboard is expected to go up near Mebane on I-40/85 next week, and remain up for a month.

   SJW, they are not at all interested in proclaiming the gospel of Jesus Christ and last time I checked that should be the focus of the Church.

   • Churches that step into the public arena like that need to lose their tax free status.

   • I went to their website, and other than a quick blurb saying Jesus was a social justice warrior, it is nothing but progressive politics: Paris climate accord, Women’s March, all coexist, blah blah. They have replaced God with government and humanism.

     I don’t worship my guns, I just want them to be treated as amoral tools, rather than the Left’s fixation with acribing voodoo black magic qualities to guns. I see metal, plastic, wood; they see demons. It really is a sickness.

     • Well, what do you expect from heretics?

       • Amen.

   • Oh, *now* churches who dabble in politics should have their exempt status revoked?

     That’s convienent. I don’t recall all this outrage happening when the megachurches stump for Republicans. Or sponsor Pro Life events. Or any number of political shenanigans that happens to coincide with the Right’s agenda.

     • and SWARF seems a pretty appropriate nic for someone who from their comment seems to lean left being that swarf is potentially damaging metal fabrication waste product

       • Swarf has been here for years. Unlike some posters.

         Plus, you know, fact is he’s (or she’s, I don’t know and really don’t care) right. If we have a problem with it in one direction we should have a problem in the other direction too, least we become as hypocritical as those we condemn.

         • yeah that is also true. personally i dont like religion and politics being mixed at all either in any direction. stay out of politics and out of the lives of anyone not in your church is my personal view. yep use funds raised by the church to help others in the local community if you want like some of the food drives for the homeless etc but political issues the churches themselves should stay out of. and no not atheist or christian or any other mainstream belief system either. as far as abortion goes while i dont agree with it there are times when i think it should be allowed eg rape cases when the trauma may affect both badly. mother because of what has happened to her and the unborn due to the suffering of the mother during the pregnancy which does like it or not affect the child

       • Great, Toni, you seem to be headed in the right direction. For your next exercise re abortion, try to assess why anybody should care what you think should happen to a pregnant woman who is not YOU! Only one person gets to make that decision, the pregnant woman involved. To reduce abortion, reduce unwanted pregnancies. There are many ways to do so, education, birth control, etc, and none are even being explored. All we hear is fanatic insistence on gaining control over someone else’s life. Has been that way for closing on 45 years now, still huge opposition to birth control or sex education, huge expenditures of time and money attempting to control young women.

         • yes i quite agree with all your points. in saying what i said i was saying that was how i felt about it personally. i also know that women that wish to go that way if it is not accessible to them will attempt backyard jobs which more often than not end up killing the mother as well. this is well documented for several centuries before abortion was legalized and part of the reason why it was legalized in the first place.
           education, birth control (not always effective unless it is abstinence from having sex in the first place 🙂 ) are means that can be used but along with that education the dangers of abortion also need to be taught as it can be a risky procedure even today with qualified doctors performing them.

     • Churches like any other organization should be able to speak out about there beliefs in politics. this counsel is so far left it Biblical roots that you would be hard pressed to actually find one thing they stand for that is accurately based on scripture. But there is no reason they should not be able to express there hatred of the Freedom found in Christ under constitution protection. if Churches are really concerned about our godless society they will not care about a stupid tax exempt status and Preach the unadulterated Gospel of Jesus Christ!

   • Nothing would excite me more than seeing churches treated the same as everyone else under the law. Make them actually earn their tax free status by being a legit non-profit organization. Right now they are just leeching off the tax-payer, a tax-payer that year after year is growing more non-religious and no longer using their “services”.

     Likewise, I see no point in electing Republicans anymore. They just passed a trillion dollar budget, more spying, more war, and a bunch of gun control at the state level. So much for “small government”. They are a joke. At this point we need to clean house and get them all out of office. Go libertarian or go home.

     • They also passed FixNICS, which doesn’t, and are proposing an illegal usurpation of congressional authority by illegal changing a statutory definition (ATF bumpstock proposed rule). The second is one of the things we constantly complained about Obama doing.

   • My church lives by the motto “Love God, Love People, Serve Your World”. They are quite happy that a number of us carry even though we’ve never once had to show our love for our congregation…

2. “Grassroots” the grass was fertalized by multi-billionaires.

   • Yep. And if her employer, bloomberg, wanted it she would be pro gun tomorrow.

3. Mini baseball bats? Aren’t those regulated under the NFA?

   • only if they are less than 16 inches long

   • Just wait until the mayor of London finds out about these, they’ll be banned in the UK.

     • They’re already close. They don’t really play baseball in Europe, but people have noticed a trend that sites like amazon.co.uk sell a lot of baseball bats right before and during riots.

       • I’d take a (full size) baseball bat over a screw driver for self defense. But it’s worthless against a gun, and if you assailant is younger (or possibly older) and in better physical condition than you, you are going to have to try and make up for that with a level of viciousness most of us have never even considered mustering.

     • Why shouldn’t they be banned there? No one plays baseball in the UK, so baseball bats have No Legitimate Sporting Purpose.

   • Mini-bats to match their mini-balls.

   • “Pennsylvania school district arms teachers with mini baseball bats”

     Well, according to ‘leadership’ in minority communities arming teachers with guns would result in teachers shooting black children.

     Where, I ask you, is the push back and fear that teachers will now beat their black students with mini baseball bats?

     Nothing? Huh…

     Professor Manque?
     Realpatriot?
     Cisco?

     Or is it just guns that would “make’ teachers commit violence against their non-white children?

4. Oh good, another ‘less than lethal’ device that looks and operates like a firearm. I’m sure there will be no problems at all with that.

   There are very few threats that cannot be addressed with pepper spray but can be addressed with pepper balls. I’m not saying they don’t exist, but few enough that I think it would be silly to start putting ANOTHER gadget on a duty belt… and they already exist in a longer form that you can put in a car.

   • I know of at least one documented case where an officer shot someone dead and claimed they thought they were drawing their Taser. I’m sure there are others.

     Seems like keeping the number of gun-shaped objects to a minimum would be the way to go.

     • Yeah the BART cop.

       The official claim was that he thought he was drawing his taser, but the fact that the draw location is different, the safety is different, the feel is different and that there is no conceivable way a trained officer could draw a firearm and think he was drawing and readying his taser, shows me that this was just the excuse they decided to go with in court to justify what was 100% a bad shoot from an undertrained, jumpy officer who should have never had a badge in the first place.

     • Robert Bates, Oklahoma deputy.

5. So Apple is looking for a new CEO? How interesting for them.

   • It’s kinda surprising to me he took that stand, actually.

     Cook is openly gay. It will be very interesting to see if his LGBT peers ostracize him for taking that stand.

     I *applaud* him for doing it, time will tell if he has the backbone to maintain that position…

     • For doing the minimum? I suppose it is something.

     • Maybe he secretly belongs to the Pink Pistols.😀

       • Check out the comment section on that SFgate Cook story.

         Pleasantly surprised by the push-back against the Leftists there.

         Lots of – “Why would they remove it? More importantly, why would anybody call for its removal?”

         And – “I’m no fan of the NRA, but Cook’s right, don’t pull their station. For the critics of this there is one simple solution, don’t watch it.”

         And – “Unreal, libs claim to be free speech but in reality are worse than Socialists.”

         And – ” Please do explain why people want to silence differing opinions? That’s the type of thing one would expect from fascists. Kudos to Apple for not bending over for fascism.”…

       • if i was in the US i would be a member of both NRA and pink pistols. i used to chat to a few members online who were members of dykes on bikes over there

       • ” i used to chat to a few members online who were members of dykes on bikes over there”

         Any chance was one of them Roberta ‘Bobbi’ Hatch?

         • not sure anymore Geoff as it was over 10 years ago now (2003-04). i remember one of them was an aussie who was the partner of one of them and who ended up back here in aus when the relationship broke up (as many both straight and gay do sadly). she was not a pink pistols member but was at least open minded enough to put me in touch with a few that were. lost contact with them cos i was off the internet for a good couple of years after that

       • Before we applaud Apple too loudly, let’s recall they took down the Manhattan Declaration from their App Store. They may allow NRA-TV, but not any content that doesn’t toe the ever-shifting LGBTQIA line.

6. A bucket of rocks in a classroom or a mini baseball bat, we are winning. They have admitted teachers do in fact need a weapon for self dense. Some of them will be wanting a gun instead of a rock to throw.

   • A gun is just a better “rock thrower!” 😉

7. (Insert “Bad Religion” by Motorhead)
   The primary thing that turned me away, and keeps me away from embracing Christianity is the fact that it is wholly and completely infiltrated by Leftists and owned by Cultural Marxists pretty much everywhere. When I was a teenager, most of my debates in favor of gun rights were with left-leaning Christians, who are the archetype for the SJWs of today. Around the age of 15, I flirted with Islam, BECAUSE of its bellicose nature, and “Might Makes Right” philosophy; this was about 3 years before 9/11/01 (which happened when I was in USMC bootcamp) but I grew annoyed with Muslims blowing up embassies, hijacking airplanes, bombing US Naval ships, destroying ancient artifacts, etc. Ultimately, I remain an atheist because religious people on the whole seem committed to illogical beliefs, and only cite scripture and rhetoric when it benefits them financially or politically.

   My only faith is in FREEDOM and LIBERTY, which most Leftists posing as Jews, Christians, and Muslims violently oppose.

   • Armed Partisan,

     Sadly, there are a LOT of bad apples in Christian churches and it poses a serious problem for the church in the long term.

     I encourage you to continue your search for truth. Perhaps it would be helpful if you concentrate your studies on teachers with impeccable credentials and track records. I also encourage you to acquire and read the book series from atheist-turned-Christian Lee Strobel where he makes a legalistic case for a Creator, for faith, and for Jesus the Christ.

     When I say “legalistic”, I am referring to the way that you would try to prove guilt or innocence in a court of law using verifiable evidence and expert testimony.

     I hope that my encouragement will serve you well on your life’s journey. Peace be with you.

   • agreed 100%. i left christianity because of that very reason. they all preached peace at all costs and disarmament of the public. BTW i am pagan and while i realize there are many pagans who lean left there are also many who are very bellicose but not in a way that would force all to their religion. they want True Liberty not the watered down liberty lite (does not exist) that most religions preach. my beliefs would be more like the Norse or the Native American Indians where those not willing to do what is needed to be done are left behind to fend for themselves and be wiped out by nature or other stronger tribes. willing but not able due to age etc is different

   • You’ve been visiting the wrong “Christian” churches…
     http://1.bp.blogspot.com/-cifwJuidbb4/UoUckAQyMBI/AAAAAAAAIY0/UoPPOYc0PAM/s1600/priest+blessing+ship+gun.jpg

     • The blessing of the cannon!!! Very old world that I like.

   • There are an innumerable amount of us that feel the same way. I don’t hate religion per se but I am highly skeptical of any person/persons with immutable and unquestionable power, especially when said power is derived from a magic sky person who tells them to tell you how to live. That being said I feel the same about government, the majority of what comes from the Feds isn’t even legislation and mostly falls into the category of “Yeah, well, that’s like, your opinion, man.”

     Let me be, I’ll let you be and I promise only to get violent if you leave me no other option.

     • agree completely. i distrust any who set themselves up as an “authority” on anything. dont care how “educated” someone is there is always room for question. also being that the “education system” since taken over by government has become an indoctrination system to keep people uneducated on things that really matter i distrust educated people more than i do uneducated or more to the point Self Educated

   • The church down the street here in Amarillo hold their men’s retreat at a nra range, the call it God, guns and food. Almost convinced me to join until the started the health and wealth crap.

   • “completely infiltrated” ? Maybe out where you are, but here in New Mexico, Skip Heitzig with Calvary Church in Albuquerque is original Born Again Christian. He reads verse for verse alternating out of the old and new testaments. Ther is an on line teaching library, explaining historical and biblical context. Wonderful! There are armed security patrols during services and supports general CC by the rest of the congregation.

     So far, I’ve seen him as not supporting any SJW or progressive/marxist agendas. There are many others like him, here and in different parts of the country, just look harder.

     • If you need to dictate the beliefs of a religious teacher, what is the point of having a religious teacher?

   • It’s illogical to know that the ratio of the radius to circumference of all circles no matter their size, is the same and presuming that is just a coincidence.

     • To me, it takes more faith to believe that everything happens by chance, than to believe that there was a creator.

       • I agree, I have an invisible, purple space orangutan that lives in my attic. Tis He who built the universe and anbody who disagrees is really doing some logical gymnastics to deny the existence of such a benevolent space ape.

       • ORCON why would you keep your ancestor in your attic? isn’t that torture?

       • All-powerful space-apes live where they want.

         He’s not being KEPT there, that’s just where he’s staying.

       • That isn’t faith, it’s called denial.

       • If we do not believe in The Creator and One God- From WHOM would “the Blessings of Liberty to ourselves and our posterity” (Preamble, US Constitution), as well as all our other liberties as acknowledged in the Declaration of Independence have come?

       • Isn’t that a “grape ape”?

   • I’d just like to point out that most leftist beliefs would be considered heresy by all mainline Christians a few generations ago. At the very least, a plurality of Christians still adhere to a church proclaiming such teachings.

     The leftist beliefs that wouldn’t be considered heresy are mostly ones that haven’t been historically considered because they are so preposterous.

8. Aren’t they worried the teachers will beat up on black kids now that the teachers are armed? Or that unruly kids will commandeer the bats?

   • Okay, Kamala, calm your tits. ;D

9. When was a teeny bat ever usefull in a gunfight ? Churches should stick to something they know ” religion ” & mother calling & weeping for gun violence victims they’re saving others ? What have you been smoking ? Drugs are bad !! Constitutional rights are undeniable. Are you all that weak minded ? Do you want to live in a society without rights ? Dispicable you.

10. I’ve seen larger drumsticks than that sorry-assed ‘baseball bat’…

11. Most young black people don’t know who Charlton Heston was. But they know who Killer Mike is. I’ve watch the reaction. Killer Mike is having an effect in a very positive way. The socialist progressives are terrified.

    • Good. If blacks adopt the 2A to the extent they’ve (y’all’ve) adopted the Democrats, the Democrats either die as a party or abandon gun control. Either one works for me. I prefer the death of the party.

      (Can’t subscribe to comments).

12. “This is not the time to do what’s easy, it’s time to do what’s right,” the governor said.”

    Vermont’s Gov. Benedict Scott just signed his replacement for this fall as the RINO for a Republican candidate.

    Benedict Scott
    This is what Vermont’s next Republican candidate for Governor had to say of Benedict’s UnConstitutional performance today.

    Oath Breaker Phil Scott signs unconstitutional S.55 bill

    A Note From Keith
    Keith Stern for Governor

    I will state forcefully and absolutely right here that if the governor illegally signs the unconstitutional S55 bill that as governor I will order my administration to not enforce it. The oath that I will have taken binds me to protect and defend the Constitution. I am sick and tired of elected officials cherry picking where the Constitution is their guide. When the McCain-Feingold campaign finance bill landed on his desk then president George W. Bush said as he was signing it I don’t believe it’s constitutional but I’ll let the Supreme Court decide. Wrong answer W. I am not looking to start an administration on an antagonistic situation but if that is the case so be it. The Constitution trumps being liked and being popular. If the legislators want to be able to work with me then they will have to repeal S55.
    Keith

    Keith Stern for Vermont Governor

    “This is not the time to do what’s easy, it’s time to do what’s right,” the governor said.”,However Un Constitutional it is.

    • Keith Stern for president!

13. Pepperball might work as long as your attacker isn’t a Cajun.😀

14. The teachers will be given mini bats to defend their class from active shooters.
    (Fine print)…………..bats will be locked up in the office, in the event of an active shooter teachers may come to the office to sign-out for a bat. If the bat master isn’t available grab ankles, kiss ass good bye.

15. I will never not love Killer Mike. RTJ 1, 2, and 3 are all absolutely stellar and his advocacy for guns is so refreshing.

16. Funny thing about those bats – the teachers and administrator may now be criminals. I think it can be argued that every one who passed out the bats and every one who too them committed a misdemeanor under Title 18 section 908 – Prohibited offensive weapons

    http://www.legis.state.pa.us/cfdocs/legis/LI/consCheck.cfm?txtType=HTM&ttl=18&div=0&chpt=9&sctn=8&subsctn=0

    (c) Definitions.–As used in this section, the following words and phrases shall have the meanings given to them in this subsection:

    “Firearm.” Any weapon which is designed to or may readily be converted to expel any projectile by the action of an explosive or the frame or receiver of any such weapon.

    “Offensive weapons.” Any bomb, grenade, machine gun, sawed-off shotgun with a barrel less than 18 inches, firearm specially made or specially adapted for concealment or silent discharge, any blackjack, sandbag, metal knuckles, dagger, knife, razor or cutting instrument, the blade of which is exposed in an automatic way by switch, push-button, spring mechanism, or otherwise, any stun gun, stun baton, taser or other electronic or electric weapon or other implement for the infliction of serious bodily injury which serves no common lawful purpose.

17. As a Christian I am NOT under the Mosaic Law. It was fulfilled in JESUS CHRIST…but I guess an apostate/heretic SJW “church”wouldn’t know or understand that…sigh. Bravo Tim Cook?!? And Killer Mike. Mebbe…

    • Technically, it’s heresy. Apostasy would imply that they no longer claim to be Christian.

      • NOT so Serge. They are one and the same. “Depart from ME-I never knew you”. People call themselves “Christian” merely for living in a so-called Christian nation. Or being born into a household that attends church.

      • Here are the definitions from the Catechism of the Catholic Church:

        2089 Incredulity is the neglect of revealed truth or the willful refusal to assent to it.

        “Heresy is the obstinate post-baptismal denial of some truth which must be believed with divine and catholic faith, or it is likewise an obstinate doubt concerning the same;

        apostasy is the total repudiation of the Christian faith;

        schism is the refusal of submission to the Roman Pontiff or of communion with the members of the Church subject to him.” [Code of Canon Law c.751]

        • I fall into all of those except the first. I have never denied revealed truth, but no invisible space pirates have ever revealed any truths to me. Other than that, do I get to choose what silly names the pompous asses in Rome call me, or is there one which encompasses all the others?

18. Glad I don’t need to get rid of my iPhone like my B of A credit card. I lose all respect for people who want to silence all who disagree with them. I can at least respect Cook.

    • I made that decision when they refused to bend over backwards for the FBI and make them a back door into their iOS security.

19. @TimCook I find it distasteful you allow Tinder on Apple TV

20. You forgot the best news of the day: Paul Ryan (who repeatedly held back pro-gun legislation) is gone at the end of the year! Scalise (who said the second amendment is “absolute”) is the expected replacement.

    • Dam i hope u are right and we still have a msjority. Would be nice to get something other than tax reform done. Secretly i dream trump resigns and Pence steps in as a real conservative. I also dream a couple of SCI might retire
      I

    • Hate to tell you but I believe they’ll try to push McCarthy on us like they did when we dumped Cantor… just to get even more “even” for not going with the elite.

21. An addition for the Digest :

    Names are being floated as potential replacements for Speaker Paul Ryan.

    One name on the list is Steve Scalise, survivor of the baseball attempted massacre :

    https://www.zerohedge.com/news/2018-04-11/top-5-possible-paul-ryan-replacements

    Sounds good to me!

    How are the other 4 on gun rights?

    • Scalise for speaker. That sounds great to me. It’ll be harder for the left to argue emotionally against a proponent of gun rights who was crippled and nearly killed by a murderous leftist.

22. How about instead of focusing on guns, you go after the idolization of Hollywood.

    • And sports stars…and rappers…

23. Never bring a billy club to a gun fight. Unless you’re Daredevil.

24. “There’s no reason for an Australian hunter to have a semi-automatic rifle for pest animal control with a 30-round magazine”
    Unless the “pest” is a squad of humans sent by government decree.

25. FCS, the 2A doesn’t _give_ anything!

    • . . . but a warning.

      And the 2nd Paragraph of the Declaration of Independence provides a promise.

26. “..training day on how to respond to school shootings.”

    So they taught them how to die with a stick in their hand? It’s almost like they understand that shootings of this nature are incredibly rare and don’t actually require any real effort to do anything about.

27. Some years back there was an article here on TTAG about training materials offered by the Federal “Department of (something)” where they advised persons confronted by an active shooter to first, hide, second, flee and, third (if forced) “try to find scissors” and stab the shooter. Another source in a State, I think, suggested Students have access to small cans of foodstuffs, like those 8 oz. cans of Tomato Sauce, and to pelt the aggressor with them in volleys. Recently, buckets of rocks. Now, tiny baseball bats? Duh! The idiots forgot “pointed sticks”…oh, wait!…I think prehistoric peoples developed rock throwing and clubbing before spears.

    So, as the jacktards progress maybe pointed sticks and then something to hurl them more efficiently are next…at this pace we’ll be up to long pointy, sharp, stabby steel things in no time at all. I guess that’s why they call themselves “Progressives”…

28. “Why Killer Mike is right: African Americans should own guns”

    I’m not so sure.

    The evil POS (D) were the ones willing to do a Civil War to maintain slavery, but stupid blacks support them with overwhelming majorities of their voting block.

    WTF do slaves need guns for?

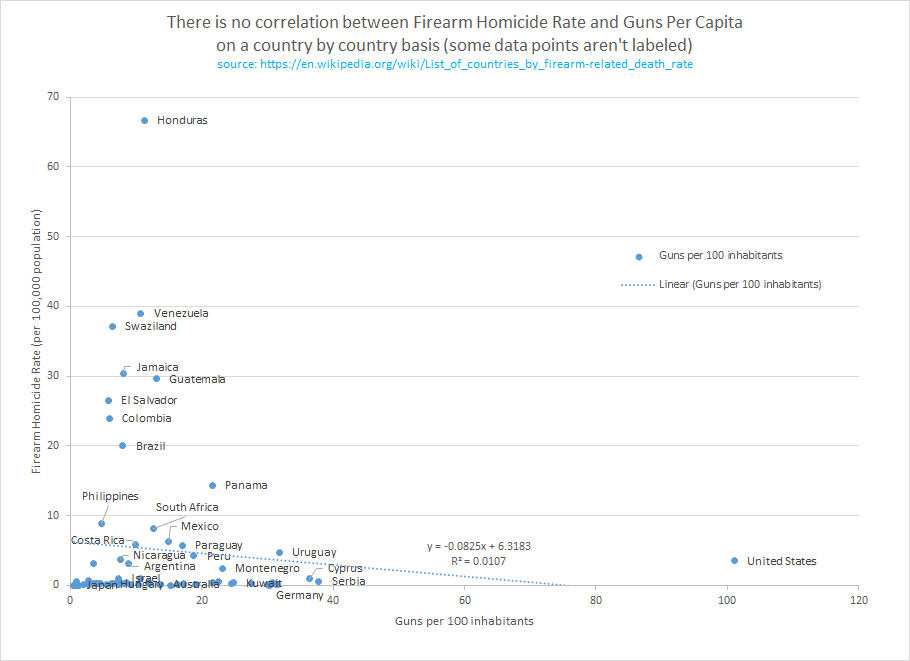
29. This is a huge deal: Everybody’s Lying About the Link Between Gun Ownership and Homicide

    This guy methodically, reasonably, entertainingly makes all the public utility arguments against gun control (and demolishes the anti’s public utility arguments while making them look like disingenuous schmucks.) And he’s not an “advocate”; not working from “Keep / ban all the guns!” to find a line of support.

    Every gun interest group, site, club, vendor should point to this.

    Double-plus propaganda points, Medium has been drifting SJ-Leftward, with creeping Zucker-pattern Twit-bans: no-platforming in the name of something, something, something. Get the meta-news, about news out there, so when they bigfoot this guy, there’s the “Advocacy much?” backlash. They have to look sane, human and reasonable to cover when they are not.

    Mothers Against Only Some Violence (and interestingly indifferent to most suicides, and carnage in the Black community) loses a bunch of its moral standing when the Bloomie funding comes out. The Childrens’ Crusade in Washington likewise lost a lot of its glamor when the median age was observed to be mid-40s. Even better by a non-aligned data-wrangling firm. (Sometimes it takes a while to graduate, but that’s ridiculous.)

    They hate being called partisans, advocates, or hacks, because then they have to go find another Edgar suit. Ruins the whole weekend.

    But, they’re advocates, not investigators. Shutting you up is as good as winning the argument — better, actually. They’ll step back from stomping out inconvenient speakers and truths, only when there’s enough cost to their facade.

    Prager got squelched because he wasn’t well known outside his direct audience, while Jordan Peterson, Diamond & Silk, & various Movie Celebs don’t get de-platformed because people know about them. Clint Eastwood may be wrong, but why are you banning him? (Get known first, make an impression as reasonable, then raise a controversial topic. Milo was doomed from the beginning given how he reached the Zeitgeist.)

    The screeching advocates see shutting up someone with BadThink as a win. The persuadable middle sees that as cheating: working the ref when you can’t win the play. You gotta make it cost the advocates enough in the persuadable middle they loose, or they’ll just take you out. “The politics of personal destruction.” as noted by the head(s) of one notable political machine, renown for its destruction of “enemies.” They hate it when you use their own tactics against them. Even a little.

    Working mention: “It doesn’t take much to demonstrate that the gun control people are about disarming citizens even when they don’t slip up and say that out loud, not keeping people from getting killed, as this one guy’s dive into the numbers shows. On Medium, here:”

    Everybody’s Lying About the Link Between Gun Ownership and Homicide
    https://medium.com/@bjcampbell/everybodys-lying-about-the-link-between-gun-ownership-and-homicide-1108ed400be5

30. This BJ Campbell guy makes a bunch of observations in his articles about manipulating data graphics.

    Deceptively manipulating data graphics can lead to all sorts of bad outcomes, like a space shuttle with people in it blowing up, when we knew better at the time.

    Tufte’s series on visualizing data is required reading. Sadly, lots off folks seem to take his inventory of misleading and deceptive practices as a “how to” catalog, not “don’t do this.”

    The books themselves are gorgeous, nearly hypnotic to read: The Visual Display of Quantitiative Information, Visual Explanations, Envisioning Information, Beautiful Evidence

    And if you want to get more outraged about commercial software infiltrating schools read his screed: “The Cognitive Style of PowerPoint” and note the now common practice of kids making a “powerpoint” as a standard class assignment … yes, it’s dumbing them down.

31. Very surprised by Apple. And not to sound sappy, this is what Saint Jobs would have wanted. The genesis of the Computer was very libertarian. This influx of social justice warriors and techno authoritarians (Dorsey, Bezos, Zuckerberg, etc) is a very recent thing.

    But the realist in me says Apple is just doing what they determined to be most profitable.

32. Here we go again: ‘Second Amendment that gives citizens the right to bear arms.’
    2A does not give us any rights. We, the people, always had the right to keep and bear arms. 2A strictly prohibits govenment to infringe this right.
    Unfortunately, the .gov has been pissing on it since 1934.
    I want my cake back!

Comments are closed.