Even the socialists? . . . In Texas, Even The Socialists Are Carrying Guns

It’s not an unusual scene when politically left and right groups mingle, except it was (David) Smith from the Houston Socialist Movement brandishing a rifle, not the red-hatted and camouflage-wearing protesters.

“Houston Socialist Movement believes that we ought to execute that right to self-defense,” Smith said. “If we’re going to ask our people to come to our events, we’re not going to let participants get hurt.”

Members of the Houston Socialist Movement, who hosted a rally against Texas Senate Bill 4, better known as the “show me your papers bill” that goes into effect September 1, have carried firearms at events before, but Saturday’s gathering in front of City Hall marked the first time the group openly flaunted rifles.

He paid his debt for a non-violent crime . . . Ex-Silicon Valley CEO, Republican Lawyer Launch Missive Over Gun Rights

A Silicon Valley CEO-turned-white-collar-criminal teamed up with prominent Republican lawyer Charles Cooper this week to launch a new offensive in the battle over gun rights.

Cooper filed a lawsuit in the U.S. District Court for the District of Columbia on Monday on behalf of Gregory Reyes. Reyes, the former CEO of the storage networking company Brocade Communication Systems, was convicted of financial crimes in 2010, including securities fraud and making false filings to the Securities and Exchange Commission.

Reyes, now out of jail and living in Montana, claims the government is using those convictions to prevent him from buying a firearm in violation of the Second Amendment.

Cooper said the filing is one in a series of “second generation” cases designed to clarify the scope of the Second Amendment in the wake of the Supreme Court’s 2008 landmark decision District of Columbia v. Heller.

This really shouldn’t surprise anyone who’s paying attention . . . FBI ADMITS Unauthorized Program Against American Gun Owners

We recently scored a major victory in the federal civil rights lawsuit Robinson vs. Sessions, now on appeal to the Second Circuit Court of Appeals.  The US DOJ Attorneys admitted in their Answering Brief that the FBI screens “all” Americans seeking to lawfully purchase a firearm against the Terrorist Screening Database (“TSDB”) upon submission of the ATF Form 4473.

“Since 2004, as part of its background checks for all potential firearms purchasers, the NICS has searched a file containing a list of known or suspected terrorists that is exported by the Terrorist Screening Center from the TSDB into the FBI’s National Crime Information Center database.”

Be at The Range at Austin‘s beautiful Patriot Club on Thursday, August 24 to meet Marcus Luttrell, The event is hosted by The Range at Austin, G2 Precision and Team Never Quit. For more information click here or email [email protected].

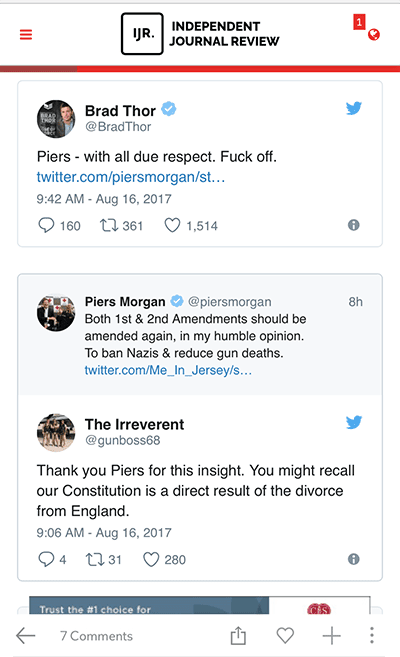
It would never occur to him that the Second guarantees the First . . . Piers Morgan Calls for First and Second Amendment to Be Changed to ‘Ban Nazis and Reduce Gun Deaths’

British personality Piers Morgan has given his hot take in the aftermath of the brutal attacks from white supremacists and members of Antifa in Charlottesville, Virginia.

He suggested both the First and Second Amendments in the Bill of Rights be “amended” in order to “ban Nazis & reduce gun deaths.”

What exactly is a “sub-military” firearm? . . . The Chilling Effects of Openly Displayed Firearms

It could have been so much worse.

Like ISIS attackers in Europe, the Charlottesville murderer used a car as his assault weapon. But Charlottesville this past weekend was crammed with anti-social personalities carrying sub-military firearms. It could just as easily have been one—or more—of those gun-carriers who made the decision to kill. If so, Americans might this week be mourning not one life lost to an attack, but dozens.

As recently as 2009, the nation retained a capacity to be shocked when individuals carried weapons to political events.

Meet The New G7 BR2500 Rangefinder

We’ve taken the best piece of gear for long range shooting and made it better. Meet The New G7 BR2500 ballistic rangefinder.

We beefed up the laser to extend range to 2,500 YARDS and beyond. This rangefinder shines at extreme ranges, while still maintaining a Class 1 eye-safe rating. We also tightened up the beam divergence to .75 x 1.5 MRAD, one of the tightest on the market and optimized for hunting conditions. We also tuned the software to get better target discrimination and detection at extreme ranges.

A-10 pilot lands plane with no canopy or landing gear after gatling gun malfunctions . . . ‘No Second Guesses:’ Selfridge Pilots Share Story of Emergency Landing

Two thousand feet up and flying over the forests of Alpena County, Capt. Brett DeVries was running through his mental checklist and most of the options were bad. With his wingman flying just feet away and an Air Force maintenance specialist patched in via a radio set up next to a speaker phone, DeVries made the decision to land his badly-damaged A-10 Thunderbolt II on the runway at the Alpena Combat Readiness Training Center.

Despite the fact that his landing gear wouldn’t come down. And the canopy had blown off the aircraft 25 minutes before. And his main radio stopped working. Along with the first back-up.

There’s an old saying in the Air Force: Any landing you can walk away from is a good landing.

In this case, DeVries expeditiously exited the aircraft – gulping deep breathes until he was certain there would be no explosion. But yes, it was a very good landing.

Don’t worry, no one wants to take your guns away . . . NY police seize veteran’s guns after order deems him, wrongfully, as’mentally defective’

Don Hall and his girlfriend were sitting in their living room earlier this year when they noticed police lights flashing outside the couple’s upstate New York home.

When the 70-year-old Army veteran greeted Oneida County sheriff’s deputies he was given a document saying that Hall had to hand over his six guns – four long guns and two pistols — to law enforcement because he had been deemed “mentally defective.”

Shocked, Hall told the police he had no history of mental issues. The deputies asserted that he must have triggered the order under New York state’s Secure Ammunition and Firearms Enforcement Act, and then the officers left with his guns.

RELATED ARTICLESMORE FROM AUTHOR

103 COMMENTS

  1. Red shirt? Really? didn’t this guy ever watch Star Trek? Oh well. I got dibs on the once dropped and only slightly bloody AK.

    • I’ll tell you boys, this man is a spy!
      He’s an undercover agent for the FBI!
      And I’ll bet he even has a commie flag,
      Tacked up in his garage.

        • Good clarification !

          “The goal of socialism is communism” . Vladimir Lenin.
          For most of the progressive/socialist “useful idiots”, they probably mean well, but the road to hell really is paved with good intentions. And if you want a foretaste of what hell is like, just go to the socialist “paradise” of Venezuela, the latest hellish iteration of complete failure that is the end result of “good intentions”.

  2. “…It could just as easily have been one—or more—of those gun-carriers who made the decision to kill.”

    It could have been, but it wasn’t. The guns nor their owners were the problem so put your projection and insecurities back in the little box you keep them in and focus on the real problems and not the imaginary ones.

    • The real problems like why were those two groups allowed within a block of each other? It’s almost like someone in charge wanted innocent people to get shot as a means to push a political agenda. But that’s just crazy talk….

      • And why were they both being led by people in deep with Occupy Wall Street if they were so ideologically opposed…

        • REALLY?

          Because the commie pinko/socialist/prog are STILL only 0.5 degrees of separation from the national socialist (“Nazi”). Too groups of rabid mongrels hyenas arguing about who is dinner.

        • I’ll tell you boys, this man is a spy!
          He’s an undercover agent for the FBI!
          And I’ll bet he even has a commie flag,
          Tacked up in his garage.

        • Well for one thing NAZIs are the Nationalist Socialist Party, so…..

          Second if you look at the social movements of the early 1900’s through the 1930’s you’ll find that these two groups actually started as a unified group with the same ideology as the 99%ers today. Once they started to grow in numbers and influence the founding leaders began to disagree and focus on slightly different methods of achieveing their goal. Then, and only then, did they become violently opposed to one another

          Now these two people are completely ideologically opposed but they both stem from a lower class social movement that focuses on tearing down the power of X wealthy class that responsible for ‘their failures’ in life and their income status

          In a nutshell they are projecting their own problems as someone else’s fault instead of taking responsibility for themselves

      • The two groups got together because the democrat party leadership in Virginia wanted a public fight. The democrat governor and mayor ordered the police to stand down.

        • @Pat….So you want us to believe that the Standard Operating Procedure for police is to let two groups of opposing people wail on each other with baseball bats without stepping in?

          Or maybe the police chief is just lying is fat ass off by saying “We weren’t told to stand down” because the mayor actual words were “Don’t do anything”.

          Also let’s ignore the dozen other Democratic cities that have similar events and were also told to not do anything.

          • I have no idea what SOP for the Charlottesville PD is. And neither do you.

            I do know that the alt-right started circulating that notion almost immediately and the local LE shot it down.

      • No kidding; it was guys in large coupes and carrying clubs & bricks that were causing the trouble. None of the agent provocateurs would dare use firearms to set off hostilities, since the authorities would not be able to keep their police passive and let the violence escalate further.

    • Bang on.

      More, not only did the gun owners *not* decide to kill, but the murderous clown using the other thing demonstrates the other thing we keep saying: people carry & wield the means to kill others all the time. What stops them is they are not inclined to, not that they can’t.

      /One at a Time
      A few years back when the SAFE positioning for a presidential run act was passed I tried having this conversation with someone who should be able to think clearly: exec of a mfg company. “What’s the point?” devolved into “People shouldn’t be allowed to carry around the means to kill each other.” Really? You think they don’t? When I asked: “So, you mean no cars, too?” Mr. not enjoying trying to support his position tried a couple times with the “Cars aren’t dangerous.” Finally he said: “I don’t feel threatened, like anyone is going to try to hit me with a car.”

      Well, unfortunately, I was right, that sheltered-guy was speaking from ignorance, and besides, wait a bit and the whack jobs will get around to using cars more, and it’ll get reported more.

      Really, he didn’t want to think about it. That we wield dangerous tools every day. That our modern life requires that: we fling around killing amounts of energy, individually, personally, dozens of times a day without even thinking about it. That any of these tools can be re-purposed to kill. That someone motivated to kill can get pretty creative. That you choose to be a fool if you don’t pay attention to what’s going on around you. Too many are just idiots and just reacting. They don’t even have a big reason.

      While we’ll never pick off the staunch anti’s, or the folks looking to borrow some authority on their coat tails (as this exec-guy was), every time there’s a conversation like this we can pick someone off in the audience. Someone who’s been cut off at an on ramp; had some clown cut them off or worse on a rush hour freeway, had some posturing muscle head flex to make a point, etc. etc. A gun is just a tool. We wield powerful tools all the time. And the world can be a dangerous place when people use powerful tools stupidly or for ill.

      • Yup, a scary thought/realization for many, that we as individual humans have the means to wield ever greater power, yet life remains as fragile as it ever was, all the while it is treated more preciously by society than at any time prior. The exact same realization has been lamented for centuries by cloistered bed-wetting philosophers who secretly desire to live as domesticated animals.

        Many people aren’t comfortable with the idea of ever operating at high-stakes. I know I frequently question my ability in that arena, and must once again resolve to be a responsible adult. But I came to the realization that the means to power –lethal force/guns– had no impact on the ultimate stakes –my life– since they were already infinite. If the stakes are infinite, you cannot afford to lose, and that means that no other factor can increase the risk further. If I need to defend my life, it does not matter what tools I have so long as they allow me to prevail, nor does it matter what tools the attacker has, since the attack itself is the threat element (the effectiveness of fists vs. pistols is but a secondary modifier, or perhaps even further removed; the attacker’s determination to kill is far more pertinent to their tactics against me, is something I cannot hope to control especially with laws, and is wholly independent of the available means to do harm)

        It’s a circular progression of thought, much like proving the Pythagorean Theorem, and seems to be self-evident to most folks who have been unfortunate enough to be subjected to physical danger. But for those of us whose fortunate life choices & circumstances kept us above that fray, it must be taught or discovered (or God forbid, learned)

      • I don’t think the crazy car killer guy in Virginia was trying to kill anybody I think he was trying to escape a mob that surrounded him and attacked his car.
        Here is a video where he pulls up to the crowd and stops, one of them hits the car with a bat and then the crowd converges on the car.
        http://i.4cdn.org/pol/1502667845886.webm

        A picture of the guy hitting the car with a bat.
        http://i.4cdn.org/pol/1502750440171.jpg

        And here is a video of the mob attacking as he tries to escape.
        http://i.4cdn.org/pol/1502666291103.webm

        • Did you see the picture of all the bodies flying through the air as well?

          It sort of lets the air out of your trial balloon.

        • Don’t worry, all the flying bodies will be put back together thanks to Obamacare and they’ll soon be back out on the street chanting their “HEY HEY, HO HO!!”

        • The road he was driving on was closed. He was directed there by other White Supremacists and drove around barriers to get on it. There is a car parked there, but it was parked there before that path was shut down to traffic. You could make the argument that he just wanted to intimidate people until they started hitting his car. But that’d be a tough sell. I think he’s just a douchebag who needs to be tried for murder, or at least manslaughter.

      • …..you forgot to incude that they’re also misogynists, islamaphobes, homophobes, transphobes, phobaphobes, etc.

      • So what? If people who hold disagreeable or even repugnant opinions aren’t allowed the same rights as everyone else, then it’s time for a new government.

  3. Piers: You guys should amend your 2nd Amendment to prohibit the arms that it protects, and while you’re at it, amend your 1st Amendment to only protect speech that I want to hear.

    Yeah, we’ll get right on it, Piers. Right after we finish giving boxing lessons to Clarkson, he punches way below his weight class if he can’t put you down with one hit.

    • Correct,Mr.Piers Moron might remember we had a revolution and his side ,finally lost ,the last and second time after 1814. He has no idea of how little we care what he thinks of America or Americans.

      Speaking of our founding,it’s is said the a woman outside of Constitution hall in Philadelphia asked of Dr. Franklin.what form of government have you given us.

      To which Dr. Franklin is said to have replied ” A Republic if you can keep it”

      In my opinion we haven done a very poor job of keeping it. GMB

    • Piers Morgan and the proud gay Andrew Sullivan both anti gun, never should have been allowed into the United States.

    • If you live in the United States, you’re almost certainly a Socialist.

      Especially if you ever intend to collect Social Security. Or send your kids to a public school. Or drive on public roads.

      Or (God forbid!) improve your health through ObamaCare.

      • Everyone is socialist and captalist, to a point. The family model is micro-socialism, were the strong (parents) take care of the weak (children.)

        And the process of picking a mate is capitalism to the letter. Where supply and demand and sexual market value are the measuring sticks of success.

      • Only because it’s forced. If the gov didn’t coercive me by means of force to take SS and other taxes out of my paycheck and I could opt out then no I would have no need to collect SS payments.

        People are waking up to the fact that Public Schools are nothing but liberal re-education camps so many are now opting out and either home schooling or sending to private schools…but again the gov makes it hard at every possible turn for people to opt out.

        And we are now forced to have insurance or pay a penalty through Obamacare.

        So don’t go on about how we’re all just happy little socialists because of the policies enacted over time by the government. The truth is that if we don’t comply and obey we are coerced by threat of force either by the taking of our wealth in the form of fines and levies or more taxes, the taking of our time by being incarcerated – and further taking of our wealth as now we’ve lost the means to produce income, or the taking of our lives by the use of lethal force if we resist.

        Yeah, sounds like a socialist’s paradise to me…

      • Yo Idaho Boy,
        Been working and paying into social security my whole life, whatever I collect from it, if I ever get the chance is MY MONEY. My two sons went to public schools and I use public roads because of the six thousand dollars I paid in school and township taxes EVERY YEAR, not to even mention the Federal taxes. What’s your point ?? A socialist is the one who doesn’t work a day in his life or do anything productive and reaps all the benefits off the backs of us hard working American Patriots. Nothing much worse than calling a good American a socialist. You need to check yourself.

      • Obamacare is the biggest lie any dip-sh•t liberal baught. Good hardworking americans having to either be forced to pay for health insurance or pay a fine ( alot I met would take the fine) because while the only ones who didn’t complain about osamacare were the ones covered by the medicaid expansion. While the liretard pillosi may get on national TV claiming it was too expenssive to force one income bracket to pay 20% there were lower income brackets who couldn’t afford to pay 15-19% uneccessary legislature wrapped in guilded paper. Just another “new deal” to keep the leftists alive. The whole gun control issue is a red herring (not the kind that sports a hammer or star) but the kind with a broken cross, and a bunch of goose stepping 88 shitbirds.

  8. Poor baby loses his gun rights because he’s “only” a white collar felon. I do support 2A rights for non-violent folks but this seems whiny…I wondered when Pierced Organ would pop up. Who decides Nazi-ism? You? Rosie O’Donnell?!?

    • Q. “Who defines Nazis?”

      A. Marxians.

      Marxians murdered 100 million people last century. Nazis murdered 10 million. Yet the universities are full of Marxians.

      Something is out of whack, and it ain’t me.

        • You know, inhabitants of the planet Mars! We just call ’em Marxians. (Or is that the planet Marx?…)

        • It’s the term preferred by academics who are fans of Marx but also want to distance themselves from the oppressive regimes and genocides committed in the name of Marxism.

          In business parlance we call it “rebranding”.

  9. Oh the sweet sweet irony of some gun carrying socialist(actually a communist since he seems to enjoy the old soviet flag) supporting policies and a system that, if it ever came into power, would seize said gun from him as one of it’s first acts.

    • Well, not if was he was in the Party, say as a gulag guard. State agents always find ways to be armed.

      • Yeah, they will call their armed supporters a Hero of the Revolution or some such BS, because some animals are more equal than others.

        • And in true Orwellian fashion they seem to rewrite history of the millions killed by their own communist and socialist governments.

          It is truly sad how completely dim these new wave of commies are. I guess there has only been a handful of smart ones because someone had to gather the useless meat for the grinders.

        • And those Heroes of the Revolution will be the second slaughter piled atop the altar of Marx. Red rather suits the Communists, since it always ends in blood with them. It has to, since they ultimately seek to confiscate & redistribute life itself, to the advantage of the Party.

  10. “If we’re going to ask our people to come to our events, we’re not going to let participants get hurt.”

    The ones who know how to shoot won’t be the ones hurt the worst…

  11. So much fail in these articles. Pierce is pathetic. You can’t ban a belief, whether or not we disagree with it, that’s against the Constitution plain and simple. So, today, neo-Nazi’s are bad (agreed), tomorrow is it Christians?

    I agree white collar felons should not have their 2nd amendment rights taken away. Violent felons should be on a case by case basis. Rape, kidnapping, murder, etc. – take ’em away forever (like that will stop ’em though). A guy convicted in a random bar fight of a felon? Maybe just for a short time after release, then gets his rights restored after his parole is up.

    Why did Repubs pass a law where officers can ask immigration status? That seems a bit third Reich to me. What should be done is they should cooperate with Feds when an ICE officer asks for an illegal to be detained, but not be allowed to ask for papers just because they are detained. Reminds me of a check point in the middle of a highway or street road. If there is no reason to be detained or pulled over – why can they stop you and ask for your papers in that case? They can’t. But it happens all over.

    • No, Christians are already lumped in with the Nazis for the most part, when it comes to the types of people that want to see ideologies banned. Oddly, so are philosophical liberatarians/classic liberals despite very secular beliefs that emphasize the individual over the collective. Pretty much anyone who isn’t an outright Communist is lumped in with the Nazis by these people, come to think of it.

    • Good call.

      Rights should be restored upon completion of the sentence. Do something you should have your rights taken away forever means you are under supervision for the rest of your life.

      Simple, really!

      {!-{>

    • This isn’t a “show me your papers” bill. It is a bill that says the local legislative body cannot prohibit law enforcement from investigating the immigration status of a suspect. The local legislative body can prohibit them from investigating the immigrating status of a witness or victim with the exception of helping them obtain a visa as a cooperating witness.

  12. It isn’t the fools standing around brandishing guns you need to fear. It’s the ones you never see…
    Those in the shadows. Silent in the darkness. Knowing the whole time that distance is their way. Waiting patiently for the right moment to wield the lightening that brings the darkness…And Yes the darkness always wins. Close up Far away Rich man Poor man the darkness cares not. Educated man Drop out matters not. The darkness always wins. So yes watch the man standing with his guns at the ready but fear the one you never see. All characters real or imagined are the rambling thoughts of the creator. But does give one something to think about. Keep Your Powder Dry.

    • Let me guess…you’re the one in the darkness?

      Because you just totally spoiled it by posting on a public forum. Now the NSA knows who you are.

      Be afraid…be very afraid…

      • Why would a facist “revolutionary” like Darkman fear the NSA now that the government is firmly in the hands of a fellow facist ?

        The NSA is the new Gestapo because facists gotta facist.

        • Remember this day and your comments about the darkness. The day will come when the darkness will take you. It’s called death son. Wasn’t being threatening and had no evil intent. seen enough death in my life. Just hoping to teach you one of life’s hard lessons. The darkness takes us all. Being a man has far less to do with the words you speak than the acts of your life. Maybe when you are an old man and lived a full and hard life you’ll understand. Words are just words. How you react to them comes in two forms. What you say and what you do. Talking is easy. Living is hard. I hope you have a long and hard life so some day you can pass these lessons on to someone else. Peace be with your soul.

      • Guess you BOYS Include PDW missed the point. Never said I was the darkness nor do I support Fascism or Revolution. My father fought in WWII to destroy Fascism. I would say neither one of you have a real grasp as to what Fascism is. Take a little time to educate yourself before shooting your mouth of. Education will set you free and might just keep you alive.

        • I did enjoy your ominous ( but apparently pointless ) “darkness always wins” speech. Very apocalyptic.

          Thanks for calling me a BOY, too. That made me laugh.

    • That guy, holding his rifle in nearly a low ready position with his finger just outside of the trigger can not be counted as a non-threat. There’s no difference between how he is holding his rifle and removing your sidearm from its holster and holding at the low ready. No difference. This goes for anyone carrying a rifle this way. I’m not sure how he wasn’t arrested for brandishing. There’s a difference between carrying a rifle slung over your back and carrying a rifle in this manner. One is open carrying a rifle, the other is brandishing.

        • Two out of four of my guns that currently have a sling attached to them are not very “operator.” The other two came with a sling, and one of those two isn’t very “operator” either.

  13. THE U.S. GOVERNMENT FOR FING

    Y E A R S

    DIDN’T GIVE A FLYING FV<K WHO THE F CAME INTO THIS COUNTRY
    NOR WHY

    But they broke their asses and their budgets harassing the law abiding free citizenry, and imposing their tyrannic bs in an effrt to "protect" us, BY FIRST ASSUMING WE'RE CRIMINALS AND TERRORISTS.

      • Idahoboy, question, what’s the appeal of a belief system like progressivism that says you are a non-entity that is only useful as some faceless cog in the mass of some “collective good” that is determined by those in positions of power?

        Like the Borg in Star Trek, or same ant in an ant hill, progressives seem to take glory in being treated with utter contempt; as being completely powerless and helpless flotsam in this journey called life with no ability to set your own course. Instead, to set your own path that is not determined by your masters; to provide, like any mature adult, your own food, shelter, warmth, self-defense and healthcare.

        So what is the appeal?

    • Minor flesh wound to the Warthog. Hell, those will be great battle scars. I suspect they’ll pop a new canopy on it, check controls and control surfaces and crank down the gear and up it’ll go again. Also, they were designed to land gear up/stowed with no or minimal damage.

      • ” Also, they were designed to land gear up/stowed with no or minimal damage.”

        Word.

        Here’s a pic of the gear (2/3 down the page) as it is in flight, half the tire is exposed:

        http://www.airplanesofthepast.com/a10-thunderbolt-warthog.htm

        Granted, landing could get dicey if he was unable to get any ordnance off the hardpoints-pylons before landing.

        But then he would be presented with a really nice necktie from Martin-Baker for pulling the handles:

        “Here at Martin-Baker, we run an exclusive club that unifies all pilots whose lives we’ve helped save: life membership of the Ejection Tie Club is confined solely to those who have emergency ejected from an aircraft using a Martin-Baker ejection seat, which has thereby saved their life.”

        http://martin-baker.com/ejection-tie-club/

    • The U.S. Army wanted to get rid of the OH-58D Kiowa Warrior. Now, they are scrambling to find a helicopter to fill the void that was left when they trashed the last good “very” close-air-support aircraft.

    • I got a question. How in the hell did it lose a canopy AND the ability to deploy it’s landing gear on the same flight?

      I suspect that somebody involved in either the maintenance or the driving of that particular bird was not having a good day.

      • It says it had a gun malfunction. If there was a detonation of a round it could have trashed all the hydraulics to take out the gear and god knows what else. The subsequent electrical problems (the radios indicate that) could have fired the canopy. I’d guess he didn’t just eject not because he wanted to save the plane but because he didn’t have confidence in the seat firing properly.

        • Maybe he attempted to eject and had a seat failure. “After a certain point, all dangers are equal” – Walter Bagehot.

          I might have attempted to land it as opposed to trying to clear the twin tail and engine intakes.

          Take-offs are optional, landings are mandatory, and any landing you walk away from is a good one. A great one is one in which you get to use the airplane again. But at least we got our pilot back. Great job!

      • Understand, the gun in an A-10 is behind the pilot, barrels extending underneath him. If a round exploded within the gun itself it could easily blow off the canopy and severely screw up all manner of other things, electronics, etc. I never heard of such a thing, but that’s sure what it sounds like. In 20 years of flying, I had exactly one gear problem, of course it was in a combat zone, taking off from DaNang. While I was analyzing, another bird tried to join on me, screwed it up and barely avoided hitting me, I’d guess less than 10 feet away and with 50 kts difference in airspeed, near out of control, that was the scariest part. After 10 minutes or so, I found a combination of actions which made my indications normal, retried extending the gear while the engines were at idle, and the gear extended normally, landing uneventful. Just sayin’, this is not a normal malfunction, especially with an explosion thrown in for good measure. He did quite a job!

        For those who haven’t, I really recommend reading the linked article, it was a great read.

    • Texas statute suggests that what the man in the photo is doing isn’t even legal. In Texas, long guns may be carried openly without a license so long as they are not carried “in a threatening manner”. While I think vague language like that doesn’t belong in laws, all charges (that I’ve found) under that clause have been for exactly what he’s doing here: carried at the ready (rather than slung or shouldered), mag inserted. Also his finger appears to be in the trigger guard, which (while it hasn’t been specifically named as far as I can tell,) as any responsible gun owner can tell you, means he’s either incompetent or he’s ready to fire in whichever direction he’s pointing it.

      All that just to say he’s trying to look scary with his rifle, which is a crime in Texas. “Openly flaunted” was a questionable choice of words, but legal open carry it was not.

  16. “If we’re going to ask our people to come to our events, we’re not going to let participants get hurt.”

    Socialists save all the hurting for after they get into power. Then everybody gets some.

        • Not quite. Any 5.56-chambered rifle can shoot .223 safely. The cartridge dimensions are the same, but the 5.56 chamber is designed to handle the higher pressures of the NATO ammo. This comes at a cost to accuracy, though, and most 5.56 rifles shoot .223 ammo pretty poorly. The .223 Wylde chamber is dimensioned differently than both .223 and 5.56 chambers, in an effort to marry the higher pressure tolerance of the 5.56 chamber with the accuracy of a .223-only chamber. By all accounts, it works, and most guys who shoot either caliber for precision use a Wylde chamber these days.

  18. It’s interesting to note the lack of pant soiling hysteria on the part of the media in regard to armed people espousing an ideology that left millions of dead in it’s wake, if it’s leftist. Compare and contrast with their panicked coverage of the militia guys at Charolettesville (who apparently weren’t even part of the rally).

  20. I would have been entertained if the Socialist/Communist was carrying an AR instead of an AK.

    • At least he’s being consistent and rejecting the benefits of the free market, by paying more money for an inferior rifle. I mean, I’m assuming he didn’t buy that AK back when they were cheap; I feel sure he didn’t own any guns before November 2016. If that’s the case, why buy a crappy AK now (you know that thing is a Century) when you can get a good AR for a couple hundred bucks less?

  21. David Smith, member of socialist group, wearing a red shirt, holding an AK.

    Sorry Smith, even leftist chicks will think you’re a jackass.

  22. I assume a socialist with a gun in Houston is there to ensure the Christians comply with the orders from the proud lesbian mayor, who ordered local preachers to produce their sunday sermons for government inspection.

    YOUR PAPERS!! YOUR PAPERS, PLEASE!!!!

  25. Hey all you Nazi symps, the only good Nazi is a dead Nazi. My grandfather didn’t go to Germany to kill Nazis, just to let the little goosestepping bastards walk to the streets of the good old US of A.

  26. California is a beautiful state – I like to look at it. My wife grew up there. We both like the ocean. But we will NEVER live there because of their stupid laws and politics. I feel badly for people who grew up in and continue to live in an anti-gun state but you have to make a decision at some point – do you want to exercise your rights to own guns without the constant threat of the gov’t taking them away or are you going to settle? I’ll stay in AZ.

Comments are closed.