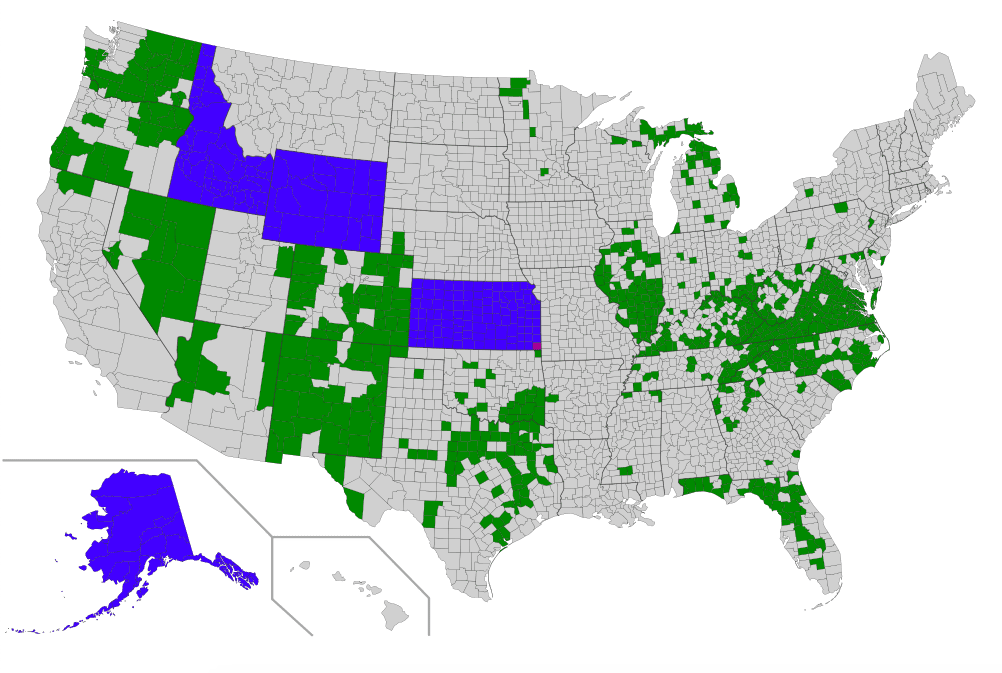
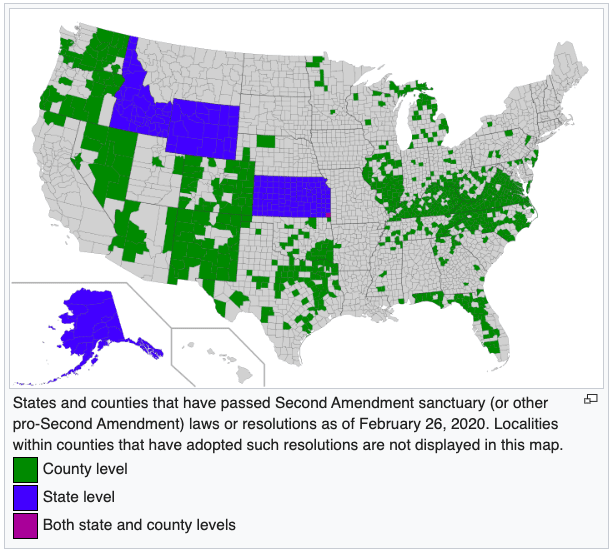
The Second Amendment sanctuary movement has spread nationally. And the tens of thousands of gun owners who showed up on the Virginia capitol steps caught the attention of gun owners who haven’t been involved in gun rights activism before. Even in states like New Jersey.
Gun owners in New Jersey argue the hurdles Trenton lawmakers have created for gun purchases don’t promote public safety.
To purchase a firearm in the state, gun owners have to pay a $5 application and provide fingerprints, consent to a mental health records check, and two references.
Applicants have to wait 30 days for local law enforcement to process the forms, but gun owners say it can take months.
Advocates argue criminals won’t wait for the state-mandated Firearm ID Card required for gun purchases.
“The criminals are going to carry anyway,” said Ron Maccri, a retired law enforcement officer who lives in Vineland. “Because they’re criminals.”
Making it harder for civilians to purchase weapons only makes them more vulnerable to criminals, said Maccri.
– Ximena Conde in The Second Amendment ‘sanctuary’ movement has arrived in NJ




That’s great and all .. but come November, go vote.
Take your friends. Have a voting buddy. Get active locally.
Large pro-gun and pro-rights crowds are fine to see and join, but at the end of the day, the elected officials we’re petitioning are elected. If not by us, who will they listen to?
Yes, turn out the vote.
Encourage all conservatives to vote.
DO NOT vote for any democrat.
Help people get to the polling place.
With bloomers billions paying people to vote and stealing elections we need all conservatives to vote.
Even if it is a “safe” district get everyone to go vote.
Last election we lost a district that had elected republicans for decades because of outside money and turn out the vote efforts by the left.
Gordon in MO,
I want to expand on your comment. Those of us who have Republican representatives who fail to support our inalienable right to keep and bear arms:
(1) Do everything in your power to replace them in the next Primary election with candidates who DO support our right to effective self-defense.
(2) Meanwhile, until you can oust your gun-grabber Republican politician in a Primary election, vote for him/her in the general election simply to maximize our chances of acquiring or maintaining majorities in legislatures.
Having a majority in legislatures is very important for a few reasons. First off, the majority party controls committees and legislative priorities. That can be the difference between bringing pro-Second Amendment legislation to a vote and burying it. Second, the majority party usually controls appointments (either directly or via confirming executive appointments). That can also impact the Second Amendment landscape significantly, especially with respect to judicial appointments. Thus, even if your politician fails to actively support the Second Amendment, he/she will probably support the Second Amendment indirectly by simply enabling Republicans to be the majority party.
I will close with this: do not let perfect be the enemy of good. We will almost never have perfect politicians to represent us. Given that reality, we must do the best we can with what is actually available to us. Refusing to vote for a politician because he/she is not perfect and enabling much worse politicians to really screw us over is bad for society. Saying it another way, winning a battle (refusing to vote for a less-than-perfect politician) only to lose the war for our rights does not serve our interests.
Some of our fellow PotG will let pragmatism be the enemy of the perfect.
Are you coming to Rally Day April 7th, 2020 at Jefferson City State Capitol.
If you didn’t vote in the last election, shut up. If you are an adult and refuse to vote shut up. Anybody who says there’s no difference between the two parties is a liar. That type of person just wants “free stuff” from the government.
The only way things will change is if you vote. Show up at these town hall meetings. You stay home. You get what you deserve.
Btw
Politicians win because they know you’re a weak a$$ MF ER. And you are an insincere person. Not willing to fight for a change. And they know it.
Plenty of people vote. On both sides of the issues.
When you’ve been displaced systematically by immigration of all kinds your vote doesn’t mean very much. That’s what the constitution was meant to prevent, a firewall against democracy which we all know is a dangerous system of 51% telling 49% to get lost, or worse.
Exactly this. The only thing I care about is my 2a stuff, and at this point, no politician does no matter what they tell too. Too many compromises. Boogaloo or die.
You retards will believe anything you hear. Good grief.
So naive.
Change comes through violence.
George Carlin advocated not voting, and in his career of 50 years he’s never been wrong. Predicted so many things that came true later on after he died, most of them related to politics
By not voting he got what he wanted. A super Leftist state in California. He talked many people into just staying home. And the crazy a$$ Liberals took over the state. That’s what happens when you stay home and you unplug. That is how Virginia got to be the sh*thole that it is now.
Now we all see just what an uphill battle it is in Virginia now, to try and stop at least some on the new gun control laws.
Carlin did say we would have “Liberal Fascism” in this country. He was right about it in several states and cities in the USA.
George Carlin was like all white Liberals. He never lived or traveled to, the areas that took his advice. Like all Liberals he lived in a very nice and expensive $$$ white neighborhood. Like all Liberals he avoided the dangerous areas that he and the others helped to create.
This! 10000 times this!
little mikey isn’t going to win…but biden’s endless bleating about gun control should be of some concern…
While no counties in Montana have declared themselves 2A sanctuaries, we are small enough population-wise to know our elected officials personally. Our sheriff here in SE Montana has stated that he will not try to take anyone’s firearms because he values his life. Not that there is much crime here to worry about.
(Soon to be gone) Gov. Bullock thoroughly regurgitated the Democrats anti-gun talking points while he was briefly doing the ‘I-wanna-be-a-president’ thing. The Missoula city counsel passes their little edicts every to often, contrary to state law. Kathleen Williams, who is running for congress again, had her full ‘I support the 2nd amendment but [insert Democrat anti-gun laws]’ thing on full display on her web site the last time she ran. None of it is there this time.
Yes, as a whole, most of the Democrats anti-gun policies won’t fly in the state of Montana. But the leftists are here and they don’t seem to be going away. Incrementalism…
I moved here for a final stand. Anyone who doubts it, fuck around and find out.
so you run your ac year round?
It’d be great to take back another blue state, but it will be hard enough just to hold the line.
Left New Jersey for several reasons…high taxes, moronic gun laws that have no effect on crime along with a Governor who is completely out of touch with the people and reality.
Let me guess you moved to the nearest Red state (or Florida) and immediately registered as a Democrat and started trying to change your new home into the same thing you ran away from hoping for a different outcome…..
Not fair. Just because someone lived in NJ, even for a long time, that doesn’t paint them with a brush. NJ was a decent place to live at one time and had low taxes and few gun laws. It even had a 18 YO drinking age.
Historical trends, odds are with 35% of registered voters being Dem vs 20% Republican and the rest as undeclared independents that vote in much the same numbers making it about 65% Dem… less than .03% declared for other parties… The primary cause for the changes in Florida and Texas from RED to fluctuating shades of purple is the influx of people who claim to be escaping the high tax and burdensome regulations of nanny states like New York, New Jersey and California that came within 500 votes of electing a full blown Socialist as Gov of Fl….. Congrats and appologies if this does not apply to you, but if you lived in N.J. long enough to remember when it WAS a red state you can understand the cynicism and frustration as we watch the same thing happening in our own homes…..
“The primary cause for the changes in Florida and Texas from RED to fluctuating shades of purple is the influx of people who claim to be escaping the high tax and burdensome regulations of nanny states like New York, New Jersey and California ”
Texas has Mexico and Florida has PR.
Those are the real feeders for the change. Sure, plenty of blue state statists moved in too but the real drivers are people from socialist countries and territories.
Fl was changing before the recent influx of Puert Ricans.. It was brought about by the migration of the bluehairs from New York, N.J, CT. to South Fl, bolstered by a rapidly growing gay community in Orange and north Polk county and now topped off by 100,000 Puerto Ricans that were automatically given voting rights in state elections (don’t look now but PR is far left/Socialist majority)
I run into people in my Texas town, who moved from CA all the time. They talk about how great it is and how much they love it, but when talk gets political it becomes clear, they are carriers of the socialism virus that infected their home state. Some are cured with time, but others are spreading the disease…
Most Mexican immigrants I know by contrast, are very independent minded and lean right politically wether they realize it or no.
90% of the californians I have ever met hated it. Maybe you are just socializing with the wrong ones.
I have learned not to laugh unnervingly at people when they tell me real socialism has never been tried. Mostly just for red flag reasons.
Okay???
But you never had to pump your own gas. How could you give that up?
Will be interesting to watch states and counties cut off salaries and pensions for the LE rebels.
“Will be interesting to watch states and counties cut off salaries and pensions for the LE rebels.”
Someone last night made a cryptic comment about a scheduled raise being shelved for insolent sheriffs in declared sanctuary counties…
Bottom line? Vote RED, Remove Every Democrat. Period. If you vote for democrats you are enabling treason.
Yeah vote Red. It makes little difference where I live in Cook County,ILL. Get politically active. Join pro-gun groups. DO NOT COMPLY! I’m bummed I can’t make fun of little Pete Buttplug anymore😃😎😏
Don’t put your joke book away yet little Pete Bootyjug ain’t done….. He will be back up on his knees looking for a spot in someones administration, running for Congress, the Senate, hangin out at Gay Days at Disney… he likes the attention too much…
The gays will vote for him any time they can.
Actually they are kind of pissed at the little guy, they claim he does not represent THEM…. Which I always thought was antithetical to being POTUS which is supposed to represent ALL Americans and not just favor particular groups within our society….
always figured they liked to be stopped and frisked….
It is imperative that people go out and vote for pro-Second Amendment Republican politicians even in districts where those Republican politicians seem to have no realistic chance of winning their elections.
First of all, who is to say that those Republican candidates cannot possibly win? Maybe they never win because a huge number of Republican voters stay home thinking that there is no point in voting — when, in fact, the Republican candidate would win if all of those Republican supporters actually voted.
Second of all, even if Democrats will win regardless of how many Republican supporters actually vote, Democrats who win with 75% of the vote will interpret that result as a powerful mandate to implement the Democrat platform. And Democrats will believe that they are invincible and can therefore enact anything and everything. On the other hand, if Democrats only win with 52% of the vote, they will see that they are vulnerable and cannot attempt to implement anything and everything.
Third, even if Democrats are virtually guaranteed to win, close races force Democrats to expend their limited resources to ensure those wins. That reduces available resources for other races where Republicans have a real chance of winning.
As a corollary to that — Delaware is a heavily blue state, and many times Democrats are running unopposed or only facing third-party candidates. The Republicans quit the field and don’t even put up a candidate. In those cases, I pick a third-party candidate is one is listed. If the Democrat is the only one listed, I pass over it, don’t vote that one at all and move on to the next entry.
The point of it is, the Democrat is going to see the total number of votes cast and maybe wonder why there is such a big margin between the votes he got and the total number. It’s the same idea you put out there — don’t give them the idea they have a mandate.
Never vote for a Democrat. Never. Never. Never.
I live in Monmouth Co., NJ and our Board of Freeholders Just passed a 2nd Amendment support resolution. The State Attorney General, an Indiana American literally had his turban explode. The boys in Trenton just aren’t used to the locals expressing their opinion.
NJ is about as close to a quasi communist based european regime as your going to find. Even CA isn’t as bad. This is a state that doesn’t even have a LT. governor. The head crook of the legislature took over when John Corazine was incapacitated.
NJ is a mafiocracy. The only difference between NJ and Putin’s Russia is the criminals are behind the scenes instead of being front and center.
In New Jersey, self-defense is a crime, even unarmed self-defense. It’s true.
New Jersey’s top gun lawyer told me, “New Jersey does not recognize a right to self-defense outside of the home.”
Someone in NJ got attacked, tried to defend himself (without a gun), and cops arrested him for self-defense and called the criminal the “victim” of his self defense!
“The State Attorney General, an Indiana American literally had his turban explode.”
Link, or preferably, a video?
whether he meant an american from indiana or an american indian why would he be wearing a turban?
“whether he meant an american from indiana or an american indian why would he be wearing a turban?”
The man is a member of the Sikh religion.
https://www.learnreligions.com/primary-sikh-beliefs-2993513
Waiting for a state or county to give this teeth. Like selling “illegal” guns at a store in defiance not state or federal “law”.
First of all, we shouldn’t have to be making any state a sanctuary state as the Second Amendment guarantees all citizens the right to keep and bear arms without question. However, where our country finds itself today politically, we must all work diligently to make every state a sanctuary state to restore constitutional gun rights under the law.
My deep blue state will never have a “2 A sanctuary county”
I’m waiting for the democrats to act very democratic with their majority and just ban mags, guns, and all the rest. I’ve got safe houses in other states and will consider my options when that happens, not if.
Why are you waiting? Better things out there. SBRs, suppressors, standard cap mags…
illinois has 38 counties declared gun sanctuary.
i thought it was more.
Good for them, but this is just more our team vs. their teamism.Once a team GOP’er suggests “reasonable” or “common sense” gun laws, the same people mobilized today will fold up like Chinese made lawn chairs under the strain of a 300lb man.
conservatives, republicans, and their politicians have shown repeatedly they cant be trusted with protecting rights. And that goes double for any armed govt employees, local cops, sheriffs police etc.
Attention mini mike et al…you mess with one of us you mess with all of us…Capice?
I’ve voted in every election since I was eighteen and that was a long time ago. Absentee ballots when I was in the army. A few years ago I had a friend that I had met in the army. No more. He was at my house and I was watching Fox news. I don’t remember the specific story but he was bitching about the subject of the story. I asked who he voted for. He said he doesn’t vote. I told him he had no right to complain. The conversation continued. Then he said, “I hate this fucking country.” I said, “Let me show you something.” Him, “What?” Me, “The door.” We haven’t spoken since. This nation has to continue after they pat us in the face with a shovel. We owe those that follow us the best that we can leave them.
“Absentee ballots when I was in the army.”
Long time back, when stationed in Texas, during a major election (don’t remember which one) there were a record number of military absentee ballots submitted. The result of the race was for Democrats. As later reported, the absentee ballots were never counted because in Texas, absentee ballots were only used when there was a tie vote, or a contest so close a re-count would be needed. Essentially, absentee ballots were surplus to just about every contest, and rarely used to decide anything. A few years later, someone told me even early voting ballots were not considered, only day-of-voting ballots. Wish I had the time available then to actually chase these matters down. Always wondered how the people in Texas permitted these abuses (if the stories were correct) to persist.
Most states still do not count absentee ballots unless there is a recount required due to a close race, Early votes are counted in Fl, I can’t speak to how other states handle those ballots..
“Most states still do not count absentee ballots unless there is a recount required due to a close race…”
Kinda does away with “every vote counts; count every vote.” Not sure there is real logic behind presuming absentee ballots would not alter an outcome that seemed to not be close, yet finding boxes of ballots in the trunk of a car is considered perfectly legit.
“This nation has to continue after they pat us in the face with a shovel. We owe those that follow us the best that we can leave them.”
Well put.
THIS! Well-done, Sir! /\
uncommon makes a bunch of quite valid and specific points. His points are well taken but I would take a more general approach as compared to his specifics.
When these people attack, by definition, they become vulnerable to counterattacks. That’s the nature of any sort of contest like this. And freedom minded people are not good at that that counterpunch, never have been.
I would point out that on a larger, more strategic, scale we have a couple of options available to us in terms of long term goals that will force the Left to oppose us and lose or support us for short-term damage control and still lose over the longer term. At first glance it may not seem connected but over a longer term it is.
Say we want to take the education system back. Well, one of the harder places to insert Lefty nonsense is in the maths and sciences. And COVID gives us that opening. It’s exposed the entire world’s dangerous dependence on China in key sectors, notably chemical manufacturing for medicine in terms of the meds themselves and the precursor chemicals to make the meds. That gives us an opening to talk education, jobs, global strategy and “national defense” every time the Left attacks on this topic.
When we talk of “manufacturing” in this country it’s mostly blue collar jobs like making widgets and cars. Here we can talk science and math because this deficiency in manufacturing requires things like chemical engineers. Lots of them.
So if Americans demand “security” in this realm what they are, by extension, demanding is a better science and math education. Our university system does that just fine but where we fall down on this front is in the K-12 system. Well, there’s your chance to simultaneously give people what they want and need while sticking it to the teacher’s unions and hamstringing the Left with a few generations of students who are inoculated against Leftist thought to a much greater degree via a science based education.
Gets us the chemical manufacturing base and greatly reduces chances for feelz based indoctrination while producing high paying jobs that create people who want to know where their tax money goes.
And the icing on that cake is the Left has two choices. Oppose science education or support cutting their own throat in terms of the majors universities put out.
“Say we want to take the education system back. Well, one of the harder places to insert Lefty nonsense is in the maths and sciences.”
You are overlooking the fact that math and science are constructs of white supremacy, white privilege. The lack of cultural and color diversity in the rules of science and math invalidate math and science as legitimate expressions of truth. Demanding everyone accept and practice a single approach to math and science is cultural oppression, destroying imagination and creativity. Even expecting all students understand even the basics of arithmetic and physics is oppression. There must be room in the nation for people who find math and science to be of no value !
Yep lefty nonsense is everywhere including math and science.
“On many levels, mathematics itself operates as Whiteness. Who gets credit for doing and developing mathematics, who is capable in mathematics, and who is seen as part of the mathematical community is generally viewed as White,” Gutierrez argued.
Gutierrez also worries that algebra and geometry perpetuate privilege, fretting that “curricula emphasizing terms like Pythagorean theorem and pi perpetuate a perception that mathematics was largely developed by Greeks and other Europeans.”
You see, math is racist, just like everything else. And every single natural disaster is because of the climate CRISIS, because there were never natural disasters prior to the industrial revolution. It’s “settled science” which, ironically, is the most unscientific thing they could say. But they aren’t trying to be scientific, they’re trying to shut you up.
“You see, math is racist,…”
There ya’ go.
There must be room in the nation for people who find math and science to be of no value !
Yes there is, they become TROLLS on the internet spewing senseless, ignorant incoherent bullshit hoping to spread their stupidity like some mindless virus whose only goal is survival at any cost including whatever credibility they might have had…..
Various discoveries in math are laid at the feet of anccient cultures, mostly in India in the 4th millennium BC, Northern Africa, Middle East and the Mediteranian (hardly a hotbed of WHITE SUPREMECY and PRIVILEGE)
Science? The ancient Mesopotamians had extensive knowledge about the chemical properties of clay, sand, metal ore, bitumen, stone, and other natural materials, and applied this knowledge to practical use in manufacturing pottery, faience, glass, soap, metals, lime plaster, and waterproofing. Babylonian astronomy, records of the motions of the stars, planets, and the moon are left on thousands of clay tablets created by scribes. Ancient Egypt made significant advances in astronomy, mathematics and medicine.Their development of geometry was a necessary outgrowth of surveying to preserve the layout and ownership of farmland, which was flooded annually by the Nile river. Plato and Aristotle produced the first systematic discussions of natural philosophy, which did much to shape later investigations of nature. Their development of deductive reasoning was of particular importance and usefulness to later scientific inquiry.. Those are absolutely the early movers and shakers of the modern White Supremacist movement.. NOT….
Props for mentioning surveying in ancient Egypt. Those guys weren’t exactly winging it.
“Various discoveries in math are laid at the feet of anccient cultures, mostly in India in the 4th millennium BC, Northern Africa, Middle East and the Mediteranian…”
Bet you will find that all the information is just a façade whites laid onto math and science to make themselves look good. But that doesn’t matter. If a culture finds 2+2=7 is a better way, there should be accommodations made for alternative descriptions of nature, and how it works. What is called “math and science” is just a prison for the brain. We need to honor and respect people with different viewpoints, not force them into a bogus paradigm. Free “math and science” to be whatever human kind can think it to be !
None of us are free until we are all free to design our own futures and realities. Rules are repression.
If you want 2+2 to = 7 no problem, just don’t go into business, I’ll gladly give you 4 bucks for 7 dollar stuff all day.. As far as rules of science/nature try gravity, jump off a 50 foot building without benefit of any external devices attached to your person or some padding on the ground and you WILL at the very least break a number of bones and at most kill yourself… Absolutes like algebra, geometry and physics are necessary in formulating engine building, manufacturing, construction, farming and anything else that requires any type of precision formulation (like making a gun function properly) The 2+2=7 crowd trying to put a 45 round in a 9mm chamber ain’t gonna work…. racist ass gun builders need to make one gun that shoots ALL rounds, rock on La-La Landers….
“The 2+2=7 crowd trying to put a 45 round in a 9mm chamber ain’t gonna work.”
Yeah? Well, I shot a 9mm round in a .45 pistol. Lived to tell the tale. So, there.
I have no doubt that you would attempt that… Must have one of those SPECIAL 45s (with the 9mm barrel?) because a 9mm round won’t chamber in a REGULAR 45 (9mm in an 11mm hole) it would just fall through.. One of those pesky mathematic rules
OK, I admit. The primer sorta ignited, and the whole thing sorta went ppffttt, and the case stuck in the barrel. All I need to do is jigger some math, and make a .45 case hold a 9mm bullet. might take several attempts to get it to work reliably, but that’s what experimentation is all about. You don’t always need white man math to make things work. The Wright brothers didn’t finish high school, and neither attended college.
I’m sorry I forgot who I was dealing with… You just keep pushing more and more bullshit that has no basis in fact.. You could not get a 9mm primer to pffffffffftttttttt in a 45 chamber because the fucking 9mm round would just fall through, the firing pin could never strike the primer unless you used math to formulate some sort of sleeve to hold the 9mm round in the 11mm chamber….
If you ever saw the Wright Bros plans for their airplane you would realize that no matter how much or how little formal schooling thay had (Wilbur actually DID finish high school), someone had instilled a working knowledge of that white mans math (algebra and geometry) as well as physics (action vs reaction) application of power vs weight…
The family’s abrupt move in 1884 from Richmond, Indiana, to Dayton, Ohio, where the family had lived during the 1870s, prevented Wilbur from receiving his diploma after finishing four years of high school. He had intended to attend YALE but an incident while playing hockey changed that…
Orville dropped out of high school after his junior year to start a printing business in 1889, having designed and built his own printing press with Wilbur’s help.
These guys were not a couple of country rubes without rescources, their father had an extensive library AND they had access to a wealth of theory, build plans and broad imaginations…
Okay, that’s it you’ve shown your ignorance and outed your intent to keep this bullshit going with nothing even remotely resembling a real fact therefore I’m going to make this my last response to you, time for you to go back to the kiddie table……
“You could not get a 9mm primer to pffffffffftttttttt in a 45 chamber….unless you used math to formulate some sort of sleeve to hold the 9mm round in the 11mm chamber….”
Plumbers putty works wonders. Gotta use the imagination, and innovate. The casing pulled all the putty into the barrel, leaving the throat clean. Neat, huh?
.
.
.
.
.
. You do realize you misapprehended the original comment, and I have been having at you, right?
Yeah Sam, and at a range officer training session I was shown the result of firing a .32 in a .380 chamber.
I have also seen someone use 7mm Remington Magnum ammo in a 7mm Weatherby Magnum rifle. Bolt was tight to close but they fire formed nicely.
“Bolt was tight to close but they fire formed nicely.”
That would be fun to see. It is all about the blast and the fireball !
One of my buds at the range got a Rock Island 1911 with 9mm and .22TCM barrels. We wanted to see the .22TCM fireball. At first, all he got was the cycling of the slide, and a sorta muffled sound. No blast and fire. After about three rounds, he broke the pistol down, and discovered the 9mm barrel was installed. FORTUNATELY, the .22TCM bullets would not stick in the 9mm barrel. After inserting the correct barrel, we enjoyed running through 50 rounds of fire and brimstone.
“You are overlooking the fact that math and science are constructs of white supremacy, white privilege.”
Sally SoccerMom and DadBod Dave don’t give a fuck about “whiteness” when Dave’s beta blockers, Sally’s eyedrops and little Timmy’s inhaler are unavailable because of China’s control of the chemical industry.
Fear can be constructive or destructive but it’s always motivating one way or another and scared people don’t give a shit about PC.
Just ask someone who’s drowning how they feel about the white privilege that a life preserver represents. See if they give a shit.
9….
Surprised you “missed it” on this one.
You retards will believe anything you hear. Good grief.
Bored waiting for the short bus, dan?
Follow The Virginia Uprising lesson and get out and vote! VA peeps sat around allowing Dems to run unopposed!
Get everyone to vote the right way to protect life through self defense!
Warren v. District of Columbia (444 A.2d. 1, D.C. Ct. of Ap. 1981) is a District of Columbia Court of Appeals case that held that the police do not owe a specific duty to provide police services to citizens based on the public duty doctrine.
In a 4–3 decision, the District of Columbia Court of Appeals affirmed the trial courts’ dismissal of the complaints against the District of Columbia and individual members of the Metropolitan Police Department based on the public duty doctrine ruling that “the duty to provide public services is owed to the public at large, and, absent a special relationship between the police and an individual, no specific legal duty exists”. The Court thus adopted the trial court’s determination that no special relationship existed between the police and appellants, and therefore no specific legal duty existed between the police and the appellants.
” “the duty to provide public services is owed to the public at large,…”
Is it not insanity that the courts hold the police owe a duty to the public, but not to any specific member of the public”? “The public” is made up of individuals. Without individuals, a “public” cannot exist? If the police owe service only to the public, and individuals of the public are due nothing, how can the police owe service to anyone/anything?
From the appearance of that map Texas looks as if it has fewer counties of sanctuary then it’s northern neighbor Oklahoma.,that’s interesting. What’s most illogical is that the United States of America has designated sanctuary areas for the Constitution of the United States of America.
Comments are closed.