With the NRA convention in Dallas over the weekend, the media have been hitting the organization, its members and civilian gun ownership in general hard for the past week. They’ve given the NRA the metaphorical full rectal examination, pointing out every flaw, blemish and polyp they could find to highlight.
HuffPost, for its part, has taken a slightly different angle on the story. They surveyed gun owners who aren’t NRA members and asked them why they haven’t joined the nation’s oldest civil rights organization.
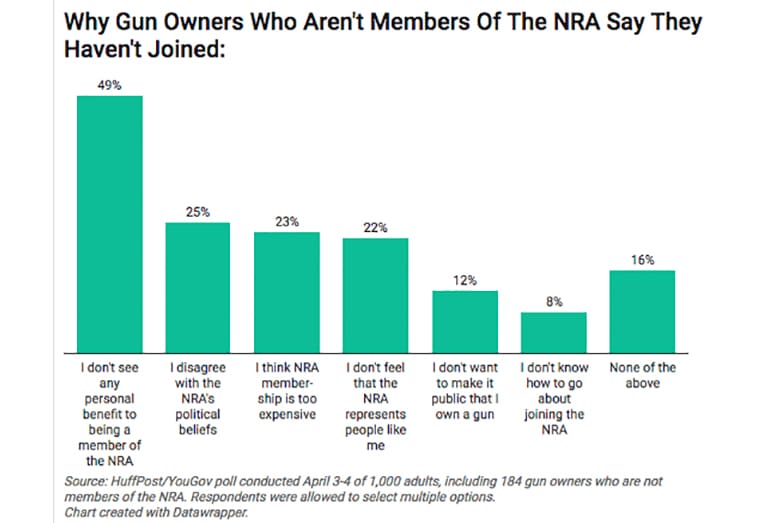
Among the non-NRA gun owners who participated in the HuffPost/YouGov poll in April, nearly half said they didn’t think NRA membership would benefit them personally. One in four respondents selected the response “I disagree with the NRA’s political beliefs” as a reason they chose not to join. Another 22 percent of respondents said they didn’t feel that the NRA represented people like them (whether that was because they didn’t feel like they fit the demographic profile of a typical NRA member ― Republican, middle-aged, white and male ― or another reason wasn’t clear). Respondents were allowed to select multiple options.
HuffPost breaks down the responses and finds that, as far as politics go . . .
A number of write-in responses criticized the NRA’s conservative stance on gun safety and close ties to conservative politics. “[The NRA has] many stupid stances; some clips and firearms need to be banned,” wrote one respondent. Others lamented the organization’s political and business ties, noting that the NRA “is the lapdog of the gun and ammunition industries,” and “a branch of the Republican Party.”
And then there are those who don’t like the face of the NRA.
Multiple gun owners pinpointed the NRA’s CEO and executive vice president, Wayne LaPierre, as the reason they declined to join the organization. LaPierre is well known for using fearmongering tactics to try to convince Americans about the necessity of guns, ranging from potential to highly improbable threats to Americans’ safety, including hurricanes, tornadoes, riots, terrorists, gangs, “lone criminals,” crime, drug gangs, Euro-style debt riots, civil unrest and natural disasters.
LaPierre’s antagonistic rhetoric has earned him enemies in high places. In 1995, former president George H. W. Bush famously published his lifetime NRA member resignation letter in The New York Times after LaPierre, in an NRA fundraising letter, referred to Bush’s federal agents as “jack-booted thugs.”
But as HuffPost found, the media pigeonhole gun owners at their own peril . . .
While the HuffPost/YouGov and Twitter polls can’t take the place of broad-scale, peer-reviewed research, the various points of view reflected in them point to a more politically diverse gun owner than is typically represented in the nation’s polarizing gun debate. That issue largely relies on the simplistic narrative that gun owners support Republican candidates and gun rights policies and that non-gun owners support Democratic candidates and gun control policies.
“It is unwise to assume that all gun owners are Republicans,” said Carson Mencken, a professor of sociology at Baylor University. Data from Baylor surveys shows that more than 20 percent of gun owners report being liberal or very liberal, while 50 percent of gun owners are conservative or very conservative, Mencken explained.
In short, there’s a vast middle/left gun ownership group out there that aren’t served by the NRA. Whether that leaves room for a new organization to fill that role — and how successful they may be in representing gun rights for those who describe themselves as liberal/libertarian/independent — is unclear at best.
But a look at the HuffPost results reveals plenty of opportunity for the NRA, too. Almost three-quarters of the respondents answered that they aren’t members because they either don’t see any perceived value in joining or think membership is too expensive. If the survey is reasonably representative and assuming a round 100 million gun owners in the US, that’s over 70 million gun owners the NRA could sign up with the right value proposition and pricing.
Then there are the inexplicables. The full 20% of respondents who either, 1) don’t know how to join(!), or 2) think that being an NRA member would advertise that they own firearms. They apparently believe that the NRA will publish the fact that they’ve joined. Or something. Again, more opportunity.
“What put me over the edge was this series of recent tragedies, both in schools and in other areas, and they just never budged,” John Liccardi, a 73-year-old hunter from Rutland, Vermont, who supported renewing a ban on assault-style weapons, including bump stocks, told the New York Times.
Liccardi, who in March penned an op-ed titled “Ashamed of the NRA” for the Vermont-based nonprofit journalism website VTDigger, wasn’t previously involved in the national gun debate in any public way.
“If there ever is going to be any progress in sensible gun ownership and control,” Liccardi explained, “it has to be from the middle ground.”
Yes, yes. The NRA has blood on its hands, hates children and eats puppies for breakfast. The HuffPost article emphasizes the NRA’s hard right political stance and opposition to further gun control laws and the like. But the HuffPost’s own research shows that isn’t even close to the reason over 80% of gun owners haven’t joined.
Is anyone in Fairfax seeing this?




No matter how much I think the NRA sucks, it doesn’t move Huffpoo off the peg into positive opinion.
What Joe R said. Took the words right out of my head.
Umm… so, I guess I might be dumb. But, doesn’t it say at the bottom of the graphic that these revelatory percentages are based on 184 people?
So, aren’t they basing their conclusions on 00.000184% of gun owners, total? Who… happen not to be NRA members. Mmkay.
Okay, perhaps it is a typo– so let’s say that all 1000 peoples’ answers are valid. So, the conclusions are based on 00.001% of total American gun owners. And that .001% are not NRA members, I guess.
Well, I went to the website– and it only specifies that 1000 people who randomly fit the “demographics of an average American” were interviewed… and that 184 people were gun owners that were not NRA members.
But even if they interviewed 10,000 gun owners… it’s still .01% of gun owners total. If there are 100 million gun owners in the US, well, 1% sample size would be a million people. That is a lot of people– and it is still only 1%. If the NRA at any given time has “5 million” members, that’s a good 95 million available opinions to extract from, and Huff is choosing… either 184, or a thousand.
And this is largely why any such “most Americans believe!” speculation with regard to gun owners is mostly just bunk. Because no matter your “intuition,” your hunch, you just can’t extrapolate public policy recommendations from .001% of anything. No matter how good or thorough the interview (regardless how unbiased it might be presented), 184 people (which I do believe is what this survey is…) or even 1000… it’s like interviewing lottery winners about the subject of luck. It’s just not a reliable sample, even IF it happens to correspond to reality (and there’s absolutely no way we can conclude that from the grossly inadequate data).
Utter nonsense. You might as well just ask yourself or your neighbir why they didn’t join… it is exactly the same. And then, there’s this:
What if the other 816 Americans interviewed were being asked why they haven’t or didn’t join the NRA– and they’re not even gun owners?
Ridiculous bunk.
Also, according to the article, the disaffected folks could select multiple categories.
How is this in any way an accurate poll where one disaffected person can vote for four categories of being annoyed while everyone else’s voice is ignored? This is only an amplifier for the disaffected, not any kind of accurate survey.
Also, in the immortal words attributed to Ben Franklin:
We must, indeed, all hang together or, most assuredly, we shall all hang separately.
You want to stave off attacks from the gun-grabbers? Then work with the organized programs or work in your community to mobilize votes against them THIS FALL. Midterm elections are in November, just six months away. The Democraps are going to push their anti-gun agendas HARD. They need to be given a bloody nose when they do so or they will keep doing it until our rights are gone.
If you’re not personally knocking on doors and making calls to get out the pro-Constitution vote, then donating to one of the pro-gun groups is the second-best option.
@ Mort
Damn man, too much thought went into that response. HUFFPOO is Fing Fake News, it doesn’t deserve the time or to see the light of day.
It’s only good to have it here so that we know what our absolute and insidious enemy is up to.
F em all.
And Cadeyrn – our Founders and Framers did hang together, now it falls to us to hang the opposition.
“There are 3 types of lies –
Lies
Damned Lies
Statistics”
Samuel Clemens
NRA wine club. Need I say more?
Everyone seems to “wine” about receiving too much junk mail/email/phone calls from the NRA. All it took was one phone call and I’ve not seen ANY unsolicited junk from the NRA. I’ve been a member for at least a decade.
I was an NRA member and left. Too many compromises over the years. Gun Owners of America has NEVER compromised and the gun-control tyrants have gone on record as saying the NRA is bad, but GOA is really, really bad! Not only that, they don’t send you a magazine. They put the money you send in for membership to work fighting for our Second Amendment rights. They only thing they send out is a newsletter which details what GOA is fighting on both national and state levels. No silly articles about which cartridge is better or which gun is best. Just pure bulldog. Remember, the NRA caved on the “assault-rifle” ban back in the Clinton era. They also caved back in the 1960s, which a lot of gun regulations first were proposed. They have a long-standing yellow streak down their back historically.
“Gun Owners of America has NEVER compromised and the gun-control tyrants have gone on record as saying the NRA is bad, but GOA is really, really bad! So- list all of the actual, real legislation run by GOA that they have never compromised on. None.
That semiauto ban you mention- how’d that work out for the gun banners? GOA would’ve never been smart enought to ammemd in the sunset provision, the bill would’ve passed regardless and today there wouldn’t be any ARs, AKs, or by now, probably no semiauto pistols either.
GOA couldn’t afford to send you a magazine, either, they use the pittance you send them to live on. They couldn’t get a policy meeting with a real US Senator or Congressman, let alone a US President if you held a gun to their heads. All BS. Easy to be “no compromise” when you’ve never had a deal in front of you… What a waste of money, time and protoplasm.
Something tells me there’s more than 50 million gun owners.
I thought it was just a couple hundred guys hoarding several million firearms apiece.
That doesn’t even include all of the dudes cranking them out in their basement. Ya think Brazil is the only place that can do finely crafted ghost SMGs?
Some people need a blue print, some just need a half-way decent mental picture.
https://homemadeguns.wordpress.com/tag/homebuilt-guns/
You can’t stop the signal. They gotta damn near kill you to wipe out all of the mental images.
“Consider, as well, the attempts to limit the possession of firearms, as a means towards
their complete and permanent disposal. The futility, and danger, of this idea can be demonstrated by pointing one’s first and middle finger at someone with one’s thumb pointed straight up and the other two fingers cupped towards ones’ palm. One doesn’t have to utter ‘bang’ for most of the population of the earth to recognize what is being mimicked.
Therefore, since the idea of firearms [a gun] cannot be eradicated, then their legal possession by the lawful must be maintained as a contradictory threat to their actual creation, possession and use by the unlawful [9]. Employing the maxim ‘I will not pay to raise up an army against myself’, hypothetically, I will not pay (provide support in any way) for you to prevent me from protecting myself against you, or other foe, who does not feel equal compulsion to support such a doctrine.
In affect, I will not support you in your attempts to disarm me for my enemies, and to preempt further shaded attacks on my security, You give up your ‘gun’ and I will get you to give up everything else. Again, this idea can be expanded to a family, a town, a city, a country, the globe, the universe.” [J.M. Thomas R., TERMS, 2012, Pg. 39]
I feel like I’ve been added to a list for clicking on that link…
I am only a member because they’re one of a handful of 2A rights organizations. I disagree with them catering to Christian Republicans, but they know who butters their bread. I’d like to see a center/left version of the NRA to try and bring the 2A off party lines.
Unfortunately a modern-day leftist group of any stripe is obligated and determined to strip you of all useful implements of self-defense.
I personally want the NRA to focus only on firearms, and grow some damn balls. No more Hughes Amendment, pass SHARE, pass NCCR, and other pro-gun efforts.
This. How, with all of this legislative and executive control we haven’t seen anything pushed through. This is an absolute absurdity.
My question to gun owners is this: Would you be willing to (actually) compromise for things? Example would be continuing the stupidity of NFA with regards to automatics, if Hughes was leveled and the registry reopened? Stamp books, each transfer paid for at POS, and stamps recorded and issued same day. If we’re going through all of these “background checks” and all of the other hassle, why is it we can’t have those things?
With the proliferation of non-nfa guns, (shockwaves, Black ace shotguns, etc) and pistol AR/AK/PCC’s, there’s zero reason to have a SBR/SBS AOW law on the books. What would be an acceptable compromise for a complete removal of that? My answer would be national standardized training, but with that, Hughes going is an absolute must. Along with that standardized training, national reciprocity would also have to be included. With the cert, nowhere is off limits (within reason, secret service isn’t going to let you in the White House with one).
You cannot get legislation passed because of Paul Ryan and Mitch McConnel.
Would I be willing to compromise if we were dealing with people we could trust? Probably – but let’s define compromise. By definition a compromise is when both sides get something the want. Not everything they want – but something they want. When it comes to gun laws, that is usually not what happens. Compromise, according to the anti-2A groups is when they let us keep some guns “for now”.
What would be a real compromise? The other side offers to give us CCW reciprocity and backs off of the assault weapons issue – and we give them expanded NICS checks. The problem is that they will never give us anything on our wish list. They would see that as a loss. Some on our side would likely say the same thing.
The reality is that, after Parkland, the other side has made their goals clear – they want them all. Maybe not now, but eventually. That’s why they will never offer a real compromise.
We have already comprised too much.
Cake And Compromise – Illustrated Guide To Gun Control
http://www.everydaynodaysoff.com/2013/11/08/cake-and-compromise-illustrated-guide-to-gun-control/
that is absolutely spot on and i think exactly why the FF wrote the 2A as they did. “Shall Not Be Infringed” instead of the wording used in most of the british documents “and as allowed by law” which gives the govt the right to legislate whatever they want. yours you have to be Willing to compromise or you can take those arms and use them against them and rightfully so. there is no such thing as liberty lite, you either have liberty or you have it not. Govt always likes to expand its powers beyond what is allowed by the people but they are smart enough to realize that if they do it all at once people will rise up and wipe them out so they take it one small nibble at a time and the put it in terms that those who are not strongly liberty minded will not see it as a threat to every other liberty that they hold dear. personally i see the right to keep and bear arms as the most important of the whole lot because it puts the power back in the peoples hands to be able to retain the rest of their rights. without the right to keep and bear arms all other rights are rapidly lost and you rapidly become slaves. slavery is very real even in most western countries. it just takes a vastly different form to what it used to take. part of the tool they use in slavery these days is taxation which is nothing but theft. there is no way you can cut it where it is not theft because if you dont pay what they demand they come arrest you, shoot you if you resist and put you in jail. it is just that the ones demanding you pay are not the ones doing the enforcing, they get someone else to do that for them
Geoff,
Not a single gun law passed since 1934 has been a compromise.
What have we gained? If we’re just giving up rights, where is the compromise? What is the other side giving up, aside from not getting EVERYTHING they want?
@Rev
That’s why I specified (actual) compromise. My question is what would we be willing to give up in order to get Hughes repealed, SBR laws tossed, National Reciprocity, etc.
@Geoff
Yeah I know, there hasn’t been any compromise at all. That’s why I’m wanting to have an actual compromise conversation.
I think the point is that since so much of our right to keep and bear arms was just taken away over the years, that many are no longer willing to give up any more even if they were to get something in return this time.
Not by any stretch of your imagination will that day ever come. I’ll speak out against the Leftards , gun grabbers , and anyone that would take my constitutional rights from me. God did not write the constitution. Our founding fathers did. Many died for the right’s we have today !! I don’t , will not , take that for granted.
‘I disagree with them catering to Christian Republicans…’
The quickest way to become marginalized is to get picky about who you keep as allies.
I am not saying they should alienate anyone. I believe they are too far into Christianity that they’re alienating people of other faiths or beliefs.
Christian values played a huge role in the fact we have a Second Amendment. Many other cultures do not believe so strongly about individual rights. I’m sure the NRA would still love their support, but if their fundamental beliefs aren’t copacetic with the 2A no amount of pandering will swing them to our side.
Personally I’m fine with agreeing to disagree where we do. I’m not even a practicing Christian, although I thank God for my good Christian upbringing. But if you’re so offended that someone might want to share their beliefs with you that you’ll burn the Bill of Rights rather than join forces to defend it, it’s not them it’s you.
BTW, this is exactly what the left is doing – turning on their own. If the Democrats don’t wake up and beg the Blue Dogs to come back they will never stop being the minority party.
quote———————————Gov. William J Le Petomane says:
Christian values played a huge role in the fact we have a Second Amendment. Many other cultures do not believe so strongly about individual rights. I’m sure the NRA would still love their support, but if their fundamental beliefs aren’t copacetic with the 2A no amount of pandering will swing them to our side. ——————————-quote—————
Look Billy Bob if you had ever bothered to read some of the statements and correspondence of the Founding Swamp Rats you would be astonished as you get the impression many were downright Atheists after they expressed their viewpoints on Religion and Thomas Paine was about as anti-religious as many Left Wingers are in modern times and remember Paine lived 242 years ago. And considering the fact that they made damn sure that they created a Government that was separated from Religious Fanatics only proves it even more emphatically.
In other words the Second Amendment did not have a damn thing to do with religion or with a bunch of sky riders in the Government.
ck, huge difference between a ‘deist’ and an ‘atheist’.
Thomas Paine was certainly not a Christian – but he was not a founding father either. Jefferson was also not a Christian – but he was a believer in God and generally believed in a Christian worldview. Most of the other founding fathers were church members and attenders. One of Washington’s first orders was to order his men to attend religious services. Trying to figure out what they really believed 225 years later is a practical impossibility.
All of that said, I would contend that it was the influence of Christianity – especially evangelical Christianity – that was responsible for the religious tolerance in our Constitution. This may sound strange, but to an evangelical, compelling someone to adopt a certain religion – even their own – runs completely counter to our theology. The only faith that matters is that adopted by choice. Yes, I know that a whole lot of my fellow evangelicals don’t seem to understand this. Tolerance is a critically important part of being a Christian.
CK yes some of them were most definately not christians and some were however they all had the same basic values that came from christianity. the all held the 10 commandments to be quite clear and a basis for law, with the golden rule coming close behind that. nope i am not christian myself though i hold similar values. i have a similar rule though it is a bit firmer and goes further. it goes “do as you will, but harm you none” it also goes on to say that if someone else is trying to harm your or yours then it is your duty to defend yourself by whatever means necessary.
“Trying to figure out what they really believed 225 years later is a practical impossibility.”
Not really, some of them left us pretty detailed accounts of their thoughts and beliefs. They had a wide mix of views on religion and were not some homogeneous group that agreed on everything, but most were Christians of varying types some of which vehemently opposed the theological views of other denominations but most of whom appear to have wanted a clear separation of church and state and freedom of worship.
Christianity was not what guided the formation of our country though, it was the ideals of the Enlightenment which focused heavily on reason rather than mysticism. Many actually believed they could understand God better if they used the empiricism and the scientific method to learn more about the world they believed he created. Read John Locke if you want to get a much better understanding of the Founders’ world views.
Randall, Rev, Cack-Sackin-Troll CK, and whoever else the fuck
Thomas Paine was very specifically a Christian, so were ALL of our Founding Fathers and Framers (maybe not all of the “signers”, but they were all more [contemporarily] Christian supportive in the same way that JFK would be considered a moderate Republican these days [if some good souls hadn’t shot his communist ass]).
America is ABSOLUTELY a Christian Nation, and founded as such. All nay-sayers are broke dick MFrs mentally playing with themselves.
Our country was founded on the premise of religious tolerance and separation of religion and government. That is not to say a Christian worldview was not predominant or influential in our laws and governance, but Enlightenment thinking was more central to the actual reasoning behind the creation of our nation and its government. In terms of us being founded as a Christian nation, the separation of church and state was written into the Bill of Rights to specifically keep our government secular, but our overwhelming Christian majorities throughout history have certainly ensured Christianity influenced our laws and culture.
You also need to keep in mind that various Christian denominations used to be sometimes violently at odds with one another, most obviously Catholics vs Protestants. Given all that, even many of the most deeply Christian men among the Founding Father’s believed government should be separate from religion.
“In the course of the opposition to the bill in the House of Delegates, which was warm & strenuous from some of the minority, an experiment was made on the reverence entertained for the name & sanctity of the Saviour, by proposing to insert the words “Jesus Christ” after the words “our lord” in the preamble, the object of which, would have been, to imply a restriction of the liberty defined in the Bill, to those professing his religion only. The amendment was discussed, and rejected by a vote of agst [against].”
—James Madison, Detached Memoranda
“Who does not see that the same authority which can establish Christianity, in exclusion of all other Religions, may establish with the same ease any particular sect of Christians, in exclusion of all other Sects?” – also Madison highlighting the disunity among Christians I noted above.
From the 1797 Treaty of Tripoli: “the Government of the United States of America is not, in any sense, founded on the Christian religion; as it has in itself no character of enmity against the laws, religion, or tranquillity, of Mussulmen (Muslims).”
In terms of them all being Christian, Thomas Paine was a deist. All you have to do is read his most famous book “Common Sense” in it he wrote, “I do not believe in the creed professed by the Jewish church, by the Roman church, by the Greek church, by the Turkish church, by the Protestant church, nor by any church that I know of. My own mind is my own church. All national institutions of churches, whether Jewish, Christian or Turkish, appear to me no other than human inventions, set up to terrify and enslave mankind, and monopolize power and profit.” Others certainly also deeply questioned the Christian faith or organized religion as a whole but none as far as I have ever read outright identified as atheists which would likely have been political and social suicide in that period. Benjamin Franklin, for example, specifically wrote that he believed in God, but he believed Jesus was a great moral teacher but not divine.
To John R.
If you think Thomas Paine was a Christian then I suggest you read his book “The Age of Reason” as he was anything but a Christian. I might add his book proves he had a great sense of humor as well although most religious fanatics would not consider his statements humorous.
From the declaration of independence: “We hold these truths to be self-evident, that all men are created equal, that they are endowed by their Creator with certain unalienable Rights…”
They felt that it was obvious that our rights came from our Creator with a capital C. The constitution does not grant us tthose rights, it recognizes those rights and protects those rights from being abused by our own government.
“The quickest way to become marginalized is to get picky about who you keep as allies.”
You are so right! I am one of those “Christian Republicans” – and I will fight alongside the Pink Pistols to preserve our constitutional rights – the 2nd Amendment in particular.
i may not be a pink pistols member (i would be both pink pistols and NRA member if i was in the US) but i would welcome you.
What was that flash-in-the-pan group of Fudds that tried to get off the ground last year? Some pathetic group that wanted to represent the Moderate Gun Owners, people who thought getting guns is too easy and we need to be more selective about who we ALLOW to own guns…
So help me, I can’t remember the name – pretty sure one of you in this audience secured the website name they were wanting to use before they did and thus denied them the opportunity to look legit (that was an awesome move).
Anyway, that would have been what a liberal-minded gun org would have looked like: supporting just about every civil rights infringement the Bigots could dream up as long as they got to keep their heirloom shotguns. We don’t need friends like that.
🤠
“I’d like to see a center/left version of the NRA”
And I’d like to see a purple unicorn singing Madonna songs while sh!tting gold ingots.
I think I’ll get my wish before you get yours.
I don’t disagree. Partially my frustration of the 2A being a partisian issue.
It’s not partisan!! it’s just one side of argument is communist gender confused baby killers out to enslave the rest of us….
When one of two parties makes gun control a major part of its program it becomes realy hard not to be partisan.
If you believe in individual freedoms, what in God’s name is appealing about the modern American left?
Are you just one of those people who finds Christianity inexplicably “icky,” even though this country was founded on Christian principles and as a Christian nation? When the Founders talk about religious freedom, they most certainly were not talking about Islam or anything else they would have considered “pagan.” Religious freedom meant the freedom to worship God (the Christian God) in any way you chose, and not have to bow to a state church a la the Church of England. Never in a million years would the Founders have imagined or expected that the USA would place “pagan” religions on the same footing as Christianity. And “separation of church and state” is a line from a letter written by Tommy Jeff, and is found nowhere in any founding document. The left, and even many on the right, have been brainwashed into thinking “freedom of religion” means “freedom FROM religion,” when that couldn’t be further from the Founders’ intent.
From my response to a similar comment above:
Our country was founded on the premise of religious tolerance and separation of religion and government. That is not to say a Christian worldview was not predominant or influential in our laws and governance, but Enlightenment thinking was more central to the actual reasoning behind the creation of our nation and its government. In terms of us being founded as a Christian nation, the separation of church and state was written into the Bill of Rights to specifically keep our government secular, but our overwhelming Christian majorities throughout history have certainly ensured Christianity influenced our laws and culture.
You also need to keep in mind that various Christian denominations used to be sometimes violently at odds with one another, most obviously Catholics vs Protestants. Given all that, even many of the most deeply Christian men among the Founding Father’s believed government should be separate from religion.
“In the course of the opposition to the bill in the House of Delegates, which was warm & strenuous from some of the minority, an experiment was made on the reverence entertained for the name & sanctity of the Saviour, by proposing to insert the words “Jesus Christ” after the words “our lord” in the preamble, the object of which, would have been, to imply a restriction of the liberty defined in the Bill, to those professing his religion only. The amendment was discussed, and rejected by a vote of agst [against].”
—James Madison, Detached Memoranda
“Who does not see that the same authority which can establish Christianity, in exclusion of all other Religions, may establish with the same ease any particular sect of Christians, in exclusion of all other Sects?” – also Madison highlighting the disunity among Christians I noted above.
From the 1797 Treaty of Tripoli: “the Government of the United States of America is not, in any sense, founded on the Christian religion; as it has in itself no character of enmity against the laws, religion, or tranquillity, of Mussulmen (Muslims).”
In terms of them all being Christian, Thomas Paine was a deist. All you have to do is read his most famous book “Common Sense” in it he wrote, “I do not believe in the creed professed by the Jewish church, by the Roman church, by the Greek church, by the Turkish church, by the Protestant church, nor by any church that I know of. My own mind is my own church. All national institutions of churches, whether Jewish, Christian or Turkish, appear to me no other than human inventions, set up to terrify and enslave mankind, and monopolize power and profit.” Others certainly also deeply questioned the Christian faith or organized religion as a whole but none as far as I have ever read outright identified as atheists which would likely have been political and social suicide in that period. Benjamin Franklin, for example, specifically wrote that he believed in God, but he believed Jesus was a great moral teacher but not divine.
to Ralph the Red Neck.
Quote——————–I’d like to see a center/left version of the NRA”
And I’d like to see a purple unicorn singing Madonna songs while sh!tting gold ingots.
I think I’ll get my wish before you get yours.———————-quote.
Several years ago I remember seeing media interviews at a gun show and the political view points ran everywhere from far right Nazi’s to far left Socialists and everywhere else in-between.
The point is the OP who advocated a center left gun organization is not far out at all but would be unnecessary if the NRA quite pandering to the uneducated Far Right and tried a more uniform approach to all gun owners.
Although to the unwashed its inconceivable that any gun owner could not be anything but a card carrying white supremacist the real facts are there are many Liberals that not only own a gun but own many and participate in hunting, competitive shooting and gun collecting. And our club has plenty of them as we have 1,000 members.
1,000 members, huh? wow
Ours is over 100 MILLION.
There are no “moderates” anymore – someone may think they are one, but absolutely no one else would agree. You either believe the Constitution as written is the law of the land (a.k.a. “fascist nazis”) or you’re a turd-eating commie shitbag progtard democrat fuckstick.
Either way, the streets WILL run red with the blood of the non-believers – sooner or later.
Jus’ sayin’
Nazis = far left Socialists, not Right.
The name of the party might give you a clue – Nationalsozialistische Deutsche Arbeiterpartei or NSDAP.
cisco, you don’t need the apostrophe in “Nazi’s” – it’s not possessive.
To Scrotum
Scoutino says:
May 10, 2018 at 06:41
Nazis = far left Socialists, not Right.
The name of the party might give you a clue – Nationalsozialistische Deutsche Arbeiterpartei or NSDAP.
I get a little tired of hearing the “unwashed” try to claim Hitlers gang were Left Wing Liberals. Its so laughable one wonders where these idiots went to school if indeed they ever did. I suggest you read “Mein Kampf” its your bible which you follow lock step with, i.e. hatred of immigrants, refugees, minorities, super patriotism, Nationalistic anti-trade views, pro war etc. etc. Its always been the hall mark of the Right Wing and the Nazis.
I think few of the “unwashed” are aware of the history of Socialism in Europe and how the Nazi’s did indeed have some socialistic programs while often reversing course and being anti-worker and anti-union while still ranting against the Communists because they were pro-worker and pro-union and they were against making war on all the other European countries. The Nazis also did not believe in freedom of the press either which was the first thing they banned as they attacked and shut down all the “Liberal” newspapers of the day. Again which is exactly the beliefs of the far right in the U.S. today. Ever notice how Trump rants against the news media just as Hitler did when he was thirsting for power.
In Conclusion Right Wing equals Nazi back in the day and now in the present. At least do not try and hide what you are. It fools no one.
meh. fecking left wing, fecking right wing. two wings of the same damn fecking bird i say. if it is totalitarian in any damn way it is totalitarian in ALL DAMN WAYS. the minute you apply force to me and say you cant do that because i dont like it when it is doing no harm to anyone (could even be smoking a cigarette) you are a god damn totalitarian asswipe. if i was smoking and you came near me and demanded i put it out i would tell you to go F your self. however if i was not smoking and you came near i would ask before lighting up if i felt the need of one and if you did i would move away while having the smoke. that is being polite.
gun rights are another matter because as soon as you compromise in any way (the NFA for example) they have greater power over you. do cops and the military still have easy access to full auto? yes they do. so who controls those groups? the govt (which always tries to increase their power and control no matter the form of govt). no matter what you say you should never trust govt in the slightest as no matter the form of govt or the number of restrictions placed on them in law they will always try to find a way to circumvent those laws and gain more power and control
If those are my only two choices, and they sure seem to be, then sieg heil, I guess.
I find it ironic people refer to Nazis being far right (especially followed up by the phrase “far left socialists”) when Nazi was a short name for members of the “Nationalsozialistische Deutsche Arbeiterparte” or translated loosly the national socialist workers party. Wasnt it untill recently that the democratic party was the workers party? Seems like the left has a consistent history of screwing over their constituents, but hey, what do I know.
There actually are some “unicorns” out there – Democratic politicians who support gun rights and the NRA. The NRA has become largely Republican because the Democratic party left gun owners – not the reverse.
I’m not sure how the NRA “caters” to Christian Republicans….but I am one, so perhaps it’s a blind spot for me.
I will say that I hate Country Music and the NRA seems to have gone all in on that 🙁
Anyway, I would truly welcome another Gun rights organization, no matter their target market, IF they truly supported Gun rights. I think that is exceptionally unlikely, unfortunately. Most likely it would be squishy on the 2A and promote all manner of “gun safety” and “common sense” garbage.
Next time I get another 10 page, “Give us money Obama is still trying to take your guns” trash mailer from the NRA I’ll skim it for the number of times Church or Faith appears. They spend a ton of money and effort trying to scare more money out of their members.
Try Gun Owners of America. The left doesn’t talk about GOA because they don’t won’t to increase its membership, and GOA doesn’t compromise. The left makes a big deal about and rails against the NRA because they know the organization is still filled with FUDs and will compromise when push comes to shove, as they have done throughout the organizations history. It is the classic scissors strategy with false opposition. It is the NRAs tendency to compromise with the disarmament people that keeps me from joining. GOA is a worthy organization and run by principled people.
Will do, thanks.
“The left doesn’t talk about GOA because they don’t won’t to increase its membership, and GOA doesn’t compromise. ” That is one of the most delusional statements ever posted, even on this site. GOA doesn’t exist, except in the minds of a few folks who have no idea how politics, our legislative system in a republic, or even human nature work. Once again, and I’m tired of repeating myself- GOA doesn’t compromise because they’ve never been in the position of creating, working and getting a bill to the point of becoming law anywhere. If you think they have- please post the examples. So far, no one has
Well, after thinking it over for a second, perhaps GOA doesn’t compromise on the cost of their memberships… That’s about it.
“I will say that I hate Country Music and the NRA seems to have gone all in on that.”
Perhaps because Country music performers are the only ones who aren’t too pussified to be seen supporting 2nd Amendment civil rights?
Half the board are CPAC board members, and Ollie North is president. And now they’re promoting ‘some’ gun control while spouting about tax law and hosting a Trump campaign rally at their own convention after he also endorsed gun control. What more you need?
Oh yeah, they also rather obviously rigged the board election against Adam Kraut so some also-CPAC slug endorsed by Marion Hammer (who also endorsed gun control) got the spot
Basically, the NRA now acts as a fundraising front for the GOP, much like the ACLU for the DNC. Welcome to irrelevant mediocrity.
And 90% of HuffPo readers haven’t the brain cells to spell “gun” without using spellcheck. Also, there are far more than 50 million gun owners in this country.
“I’d like to see a center/left version of the NRA to try and bring the 2A off party lines.” If that would ever happen the left, particularly the democrats would first have to drop disarming the American public as being one of their top three issues. (The other 2 would be contiuning to flood the country with illegal aliens who jump the fence with no documentation and raising everyone’s taxes so they can give it away to the factions that they believe would vote for them.) I don’t see this happening in my lifetime.
To paraphrase, there’s a vast middle/left group of gun owners who don’t give a shit about the 2nd Amendment. We’ll just call them Fudds for the sake of brevity.
The NRA caters to OFWG and republicans because we care about our rights and vote accordingly. I’ve talked to black folks saying “the NRA lies about Obamas” and other such drivel. I don’t give a rat’s azz about leftard rights. After Newtown I was OK with old Wayne-now he needs to go. Methinks we’d have a pantsuit Hildebeast occupying 1600 Pennsylvania without the NRA. The NRA should have many millions more members…
I find puppies are tender and tasty. Some ghee and garlic heated in a pan, toss in some onions and fry it up.
Beagles taste better with cream cheese and lox.
“In short, there’s a vast middle/left gun ownership group out there that aren’t served by the NRA. Whether that leaves room for a new organization to fill that role — and how successful they may be in representing gun rights for those who describe themselves as liberal/libertarian/independent — is unclear at best.”
The NRA is a one issue organization, liberal/libertarian/independent are not one issue. The three L’s, Libertarians, Liberals, left and Independent will vote for gun grabbers. The civil right to arms is low on their priority list.
They want all or some of the following. Free condoms, free health care, legal marijuana intoxication, and the ability to legally shoot up crystal meth to improve their sexual experience. That is why they vote democrat. There is nothing the NRA can do to attract these people.
They are an example of most gun owners in California. I say this because I’m a former resident of that state.
I don’t think you understand what a Libertarian is supposed to be: one who believes in the maximum amount of personal liberty with the minimum amount of governance to make it happen. Libertarians are supposed to be hardcore 2A supporters and pro-marijuana and believe that you should be held accountable for evil actions or those that harm others, but never for the mere possession of inanimate objects. The opposite end of the spectrum from authoritarians, whether left or right. But the Libertarian Party has indeed had nothing but shitty candidates for the presidential race, so I understand where you might be confused.
I’m a libertarian and the NRA is too soft on the 2A for me. They do nothing but “compromise,” i.e. give our rights away slowly over time.
completely agree. i am not overly fond of the Libertarian reps here in australia either. they are for big immigration (and not fussy from where, if the cultures were compatible with ours then i would not care quite as much), and they are for the big multinationals that are part of the problem. sure they are not so bad in many other areas but as much as they are staunch on gun rights those other 2 are also a big downfall IMHO
The Libertarian Party had Austin Peterson, but the Manchurian Candidate Gary Johnson somehow won the nom instead. Austin is currently running for US Senate, and part of his platform is making machine guns legal again. THAT’S a Libertarian.
The NRA is far too liberal for me, and I don’t appreciate all of the BS they stamp their approval on that gets passed, like the 86 GCA, the NFA, etc. With all that we’ve lost at this point, any mention of “compromise” needs to get us a win as part of the “compromise”. SHUSH act, maybe national reciprocity (if done right, which the NRA wouldn’t), repealing the unconstitutional Hughes amendment… But the NRA doesn’t seem to care about regaining lost rights, only about slowly losing the ones we have left. No thanks…
That doesn’t mean the NRA doesn’t do good work, but I’d rather put my time and money elsewhere.
I’m not a member because the store I bought my guns from (turners..) sold my name and address to their mailing list and I never asked to receive their junk mail. Last month, they sent me some membership card and I sent it back with writing on the envelope, black sharpie, to take me off their list and leave me the hell alone. If they hadn’t sent any junk mail when I’m trying to stay below the radar and live privately, maybe I would have joined.
I am no longer a member because they left CA high and dry right before 2016 anti gun bills went to vote. I’m still a member of Guns of California and California Rifle & Pistol Association. These folks keep up the fight behind enemy lines.
And here we thought the NRA was an evil empire of all gun owners that told gun owners how to vote.
If they focus on the NRA too much they might find themselves outflanked instead by the rest of the gun owners.
I gave up on my NRA membership after I got renewal notices a month after I re-upped my membership. I got a constant barrage of “alerts” implying that the jack booted thugs were going to kick in my front door, rape my wife, and shoot my dog if I didn’t immediately send money their way – and this was back in the 80’s. I agree with the NRA’s goals but their constant overwhelming hysteria is just too much to deal with.
I was a member of the NRA despite things I didn’t like (excessive religious rhetoric, automatic support for the police even when they don’t deserve it, licking Trump’s boots even though he’s not a real 2a supporter, etc) but I cut up my card and mailed it in when they announced that they choose The Felonious Oliver North for President. Time to send a check to GOA.
76th board member election was also rather obviously rigged.
Ted Nugent is a POS.
And you have done, what, to further our cause?
Don’t dump on people just because you don’t like their music, yadah, yadah….
Either get on board or get the hell out of the way. Doing nothing will get you ran over, by the Left or the Right.
Let’s see…I’ve become a state certified firearms trainer so I certify people to get the CC license. I open support local groups for CC and run independent response training.
Nugent is a hypocrite. I’m driving the train.
I used to like Ted Nugent when I only knew his music.Now that I’ve gotten to know him better he’s a straight up fake in my books, and it ain’t got nothing to do with the NRA
People who are gun owners and do not belong to the NRA are composed mostly of skin flint cheap ass and uneducated Red Necks. As a matter of fact well read people and people that are products of higher education are far more likely to join simply because they are very familiar with the “entire” history of the NRA not just some of its failures.
As I have said before only an ignorant cheap skate Red Neck would have fired George Patton in WWII just because he did not please everyone all the time especially considering his military record. Patton screwed up too but he was kept on because he was the right man in the right place and at the right time. And so was and is the NRA. If any of the “unwashed” think that any of us would own any firearms today if it had not been for the hard work and the majority of times when the NRA won against many of the antigun assaults on our rights the “unwashed” are only shouting to the world what uneducated Fools and cheap skate Morons they really are.
If the NRA fails to win or please you all the time the most you lost is a measly 30 Bucks but if there is no NRA or if it does not have enough funds for the fight then you lose all your guns which is a hell of a lot more expensive than losing just 30 bucks.
Now you cheap ass ANTI-NRA Idiots what part of this do you not understand. Because this is the real reason you never joined and you fool no one but yourself. Its the mark of the true Hill Jack which is “I am too much of a cheap ass to spend a penny today even though I know that I am going to lose everything tomorrow”.
Wow, who put the quarter in you?
Seriously, you made a few very good points.
So, how do you get people to pony up?
I largely agree. Some are cheap and some are missing the forest for a tree.
I’m upset they compromise. I’m unhappy they pay their all stars huge money, my money. I’m tired of the Sky is falling rhetoric and over the top scare tactics. But I also know they are the big gorilla and that they hold clout in DC.
You lost your respectability when you wrote your first sentence which shows just how little you know and are. As for your second sentence, I fall within the higher educated and am not a member of NRA as is my choice.Your calling a person who is not a NRA member: ( “unwashed,uneducated,cheap skate morons” ) only shows how ignorant YOU are. You are not worth any more of my time because, I now know you do not get it and never will. Stay safe hiding behind your computer.
Whole lotta people bought Life just so they could vote for Adam Kraut and make a dent in the corrupt leadership exemplified by Marion Hammer (favors gun control, takes numerous paychecks from NRA-funded local groups that do no advocacy). Whole lot of folks at the convention stumping for Adam, the only candidate I even heard mentioned, actually.
Somehow he got no more votes than last year & was defeated by an 80 year old nobody who got 8X as many votes as last year despite no online or comvention campaign presence whatsoever. He was simply endorsed months back by Hammer while she called “radicals” like Kraut “The Enemy Within”
Damn right I’m too cheap to waste money on that shit.
Crisco, are you educated? If so, you should ask for a refund. Your writing is barely 6th-grade level, rife with misspellings, poor syntax, punctuation errors, and an overall lack of logic. Seriously, you’re always mocking those who disagree with you as morons, ignorant, uneducated, redneck (one word, moron), etc., yet you clearly are all of those. These aren’t typos (a common excuse from idiots), they’re just an indication of poor education.
Cisco, wow.
did the Soros paycheck get lost in the mail this week?
Oh looky, Crisco Kid, the angry keyboard faux intellectual.
Wow. Megan “the kid” Kelly has a point and I agree. Those who bash the NRA are generally ignorant of its history and specifics of its many legal challenges.
Btw Megan your analysis of Patton is on the money. I’ll withhold my methamphetamine comments for now.
The center/left version of the NRA SHOULD BE the damn ACLU. How they can defend all other civil rights, including invented ones, but ignore the Constitutionally-enumerated 2nd is beyond me.
It’s because they were co-opted by the DNC and shed their legitimate mission to be fundraisers. Just like the NRA is now choosing by wedding itself to the GOP.
Tex Ted you probably do live in Texas your education level proves it.
quote————————–The center/left version of the NRA SHOULD BE the damn ACLU. How they can defend all other civil rights, including invented ones, but ignore the Constitutionally-enumerated 2nd is beyond me.——————-quote
The real facts are the ACLU has stood with the NRA and gun owners in the past on some issues. Here is JUST ONE OF ONE OF THEM.
https://www.csmonitor.com/USA/Justice/2016/0624/Why-the-NRA-and-ACLU-take-same-side-of-no-fly-gun-debate
Many Americans exercise 1st, 4th, 5th, etc rights, but less than 2 million of them members of the ACLU. Why do 99% not join the ACLU?
When I see the NRA using all their money and influence to help me out here in MA, then I might throw some more money their way. Until then, they’re little more than a useless group of dumb rednecks.
More like bluebloods, actually
Fuck You Huffpost you don’t know shit.
How is ‘junk mail’ not its own column on that chart?
The important point is that gun owners have enemies financed lavishly by Bloomberg. The NRA, while imperfect, is our best defense against him.
I belong to the NRA, GOA, NAGR, Guns Save Life, Inc, and the Illinois State Rifle Association. We can’t to too active in fighting the gun control bigots.
What is up with the word “hunter” being synonymous with “gun grabber” in the news as of late? I am starting to think that we should try to start banning hunting rifles over “assault rifles” so these asshats will wake up and put some skin in the game to defend our rights.
When it’s the hunting rifles’ turn, they’ll just call them “high-powered sniper rifles”.
GOA, 2A Foundation, FPC, CRAPA and next payday, Gun Owners of California. Ain’t that enough? F The NRA, till Wayne, Chris and their leg humping followers (FUDDS) are long gone.
You all keep wanting another gun rights organization.
Have you forgot the GOA, Gun Owners of America and the Second Amendment Foundation, the JPFO Jews for the Preservation of Firearms Ownership, NAGR National Association for Gun Rights, all the different State Carry Organizations.
Well, I disagree with the NRA’s political beliefs and don’t believe they represent people like me.
The NRA is all to eager to appease and concede. What have we gained for all the concessions that have been made since 1934? The privilege to keep an ever-shrinking percentage of our rights?
Interesting. The non-members who don’t point out not joining due to politics are immediately tagged as “middle/left” by the professor. I opine that they could just as likely be “middle/right”. I don’t see how he would know.
HuffingGlue can kiss my NRA membership ass.
And any gun owners who hasn’t joined the NRA (and can afford to) is an uninformed boob.
I want to see a survey of non subscribers to the Huffpost, and their reasons for not subscribing.
Not much more to contribute, but When I was teaching Basic Pistol to as may as 36 students a year, I would include a one year membership in the NRA with their certificate. Many of those students got tired of getting dunned for contributions weekly and told me they would NOT renew due to the junk mail. I brought this up with Col. Land when he was Secretary of the NRA and he told me that as long as they make any money on the mailings they would continue.
NRA is no different then ARRL for Ham Radio and AOPA for Private Pilots. Only a small percentage will join. We need to keep the NRA strong because they are the MOST EFFECTIVE lobby for our rights.
The NRA provides training which has significantly reduced gun deaths.
As for the FUD comments, I do not hunt, but I prefer the FUDs to the guy who who collects plastic fantastic pistols and while I own AR style rifles, seems that many who own them (as seen on the range) seem to be wannabes.
I would have never joined but for the fact that the rifle range near me (an honestly perfect range for all forms of firearms and even crossbows and archery) required membership to be able to join the club.
I just think the NRA is slippery about what they do for their members after they pay their membership fees. It’s the little things, like advertising a benefit of joining to be a really nice folder, then never sending it until you make three requests and when it arrives you couldn’t open a letter with it.
Little irritants like that suggest to me that they really only want the money.
If u don’t belong to one u should be pistol/rifle whipped really bad…. and have all ur guns taken and giving to someone who is fighting for the rights of all Americans!
NRA has been giving stuff away(Our Rights) b4 the anti’s even asked! But, there are many other gun rights groups like the #GOA #SAF
I ain’t giving them nothing. My Rights are not for sale.
What other right is taxed and u have to ask permission to buy a gun from Uncle NICS?
Getting a gun can be costly in those crap hole states!
Lets apply that antigun logic to free speech! Just give up all ur cool words and pay a dollar for every word u speak or read on the innerwebs…..its for the children.
Personally I’m of the opinion that the NRA isn’t hardlined enough. If you’re completely honest with yourself they’ve dropped the ball over the years… A lot. That said, had they not been there at all, things would’ve been unforeseeably worse for gun owners today. I’m a life member even though there’s a lot wrong there on political whims and what have you, because they are the single loudest voice we have to unite behind. Likewise I know many people, not nessesarily all gun owners, who support the second amendment AS INTENDED (not “I support the second amendment BUT”(If this is you, you don’t)) and thus support the NRA with donations if not words but aren’t members in either case. I also know people who don’t support the NRA at all because they aren’t “radical,” enough; like my opinion, “not one inch.” Coming from California, that should say alot.
Wish us luck, we need it here.
i agree with you completely. here in australia i have to be a member of SSAA to keep doing my shooting sports and that is not even allowed any defensive use…. sporting only! our SSAA dropped the ball big time and has since too. i have considered joining the NRA myself even though i am not in the US but i see their failings as well. time for a big shakeup in the board etc and get members in there who are no compromise and who are straight down the line as the 2A states….. if not then there will be no other way than CW2 and that will be downright nasty.
I have hopes for the most part here in the US, the major good thing is that Trump is putting in Supreme Court judges that aren’t leftist political activists and they will interpret the constitution as intended and written. California on the other hand, I wouldn’t put it past them to write up a law making ownership of anything semi auto a felony, and pass it tomorow without vote. Its been clear to me for over a decade our local government prefers felons to law abiding tax payers(I’m 21 so thats how you know how bad it is). I don’t know a ton about the Australian constitution in regards to guns but sounds like you guys need 1: non career politicians, and 2: your own second amendment. If it doesnt work out there, come out here, we’ll be glad to have you, legally of course:) Personally Idaho is where I think I may be headed but remains to become a thing.
Many of the comments written here simply confirm my belief that a lot of non-gun owning trolls hang out here to spread rumors and distrust AND there are some dumb gun owners. The ONLY reason we still have the gun rights we do is because of the NRA and it’s supporters. As someone earlier mentioned they are still the “gorilla in the room.” I don’t care if you agree with their tactics – I don’t like some of their tactics – they are the ONLY organization with any serious clout on the Hill. Look how afraid the left is of the NRA and how much they blame them for everything bad that happens – that alone should tell you how effective the NRA is in fighting for our 2A rights. Pry open that wallet and join.
As i have said several times if i was more financial i would be joining the NRA despite not being in the US. i would also be joining Shooters Union here in australia (which is an NRA Afilliate) and also Firearms Owners United (FOU) here in australia. those 2 do far more for shooters rights here in australia than SSAA ever has though at this stage SSAA is the largest and in many places the only “legitimate” membership to own a gun in the country and has most of the gun ranges. there are a couple other gun ranges here in alice but none of them have the range of disciplines available that SSAA does
Do your research. Look it up yourself. The NRA has caved many times, supporting the National Firearms Act of 1934, the 1968 Gun Control Act, and lastly, the 1984 Brady Act. Don’t take my word for it. Ask the NRA. No doubt you won’t find such double-dealings on their website because who could get members with a record like that? I know, I used to be a member. Joined Gun Owners of America because all they do is fight for our rights and they have NEVER compromised. They don’t waste my time with pretty magazines that have nothing to do with fighting for my Second Amendment rights.
You about covered it with your examples. Thats the biggest thing right now with the NRA, getting their head out of trying to find a midle ground and hold their ground instead. Back in 34 people were alot more complacent since firearms were evolving at a break neck pace and grand pappys 94 Winchester was the “ar” of its day. You can thank the Clinton AWB for the gun culture of today, nobody cared about automatics untill they suddenly weren’t allowed to have them. Thankfully people have woken up since then.
What I take away from this is that many gun owners don’t join NRA for one of two reasons, neither very flattering for the non-joiners: either they are ignorant of current politics and can’t see through the rhetoric of the gun-grabbing crowd, or they are cheap, unwilling to shoulder the burden of defending their own freedoms. Then there are the truly benighted lefties like the clown who said “some clips and firearms need to be banned.” He’s a gun owner but doesn’t know the difference between a clip and a magazine. Really? And finally there are the truly asinine, those like old man Bush who say their own way or the highway. (Personally, all I need to know is that a member of the odious Bush mob rejects membership to know I REALLY want to belong to any club or organization.)
John, I never realized that being a member of the NRA automatically made a person an expert at everything. Did you ever think for just a second there is a third reason a person may have for deciding not to join the NRA? First let me say, as a gun owner I am neither ignorant or cheap. In fact, by your dialog you truly show how uneducated you are on many different levels. Just for your info, I spent 28 years of my adult life defending mine,yours,and the rest of Americans freedoms. I do not need to put my money up to join the NRA to prove my loyalty because I have put up something of real value, my life. With that being said, it is people like you with your misguided beliefs that not belonging to the NRA means we are worthless. Just remember, you have your 1st amendment right and all the rest of your amendment rights because of the individuals who were willing to shoulder the burden to defend these freedoms even though many are not NRA members. Just for a little satire to show you things can have different meanings: CLIP-What you get when you go to a barber shop// MAGAZINE- What you read while you are waiting to get a clip. Now when talking about guns: CLIP- Holder for rifle cartridges: MAGAZINE: Compartment for holding cartridges in a gun. Hope that information has taught you something since in your comment you stated ” Really “. To conclude, I for one do not need to join the NRA to prove anything and especially to you a person who opens their mouth before taking the time to gather the complete facts.
lol i have a rifle that uses a clip (holds 5 rounds inside and outside of magazine) but without which the rifle is effectively a single shot. you push the clip down into the Fixed magazine well and it locks there till the last round is chambered and the clip drops out the bottom of the magazine well. it is the old Austrian M95 Styer in 8x56R. most rifles designed to use clips the clips are simply stripper clips and usually have a indent to take the stripper clip at the rear of the (usually) Fixed magazine well and you strip the rounds out of the clip straight into the magazine. in a combat zone it can be somewhat more efficient way of loading the magazine than having a box of loose cartridges. the lee Enfield also used this method despite the fact that the magazine was in itself removable. a clip is usually cheaply designed to be disposable/throwaway while a magazine, removable or not is designed to be reused many times. hope this explains the difference somewhat.
Of course, if one wants to put HuffPo’s figure into perspective; very few of all elligible voters actually belong to a political party in the US. Americans are not, by their nature, “joiners” in anything that requires one to declare and put something on the line. When actual polling is done, however, particuarly when the gun banners are making a lot of noise, something like 40% of those polled claim to be members of NRA, and NRA’s “favorability” is often well-above 50% of all Americans when the dust starts settling, reality settles in and people start thinking for themselves again.
Sitting at the door of large gun shows, everyone entering must pass us and nearly all claim to belong to NRA, which is total BS. Actually, by my estimates, HuffPo is off by about 5%- only 5% of gun owners belong to NRA. In light of that, it’s amazing Americans still enjoy more God-provided 2nd Amendment-type rights that anywhere else on the planet, unless you count an island or two owned by the mob, and then that only covers their guns.
Comments are closed.