America’s Obsession with Powerful Handguns Is Giving Criminals Deadlier Tools. That’s the headline above a post by Alex Yablon at thetrace.org. The article implies that if you own a “powerful handgun” you bear responsibility for criminal access and misuse of these “powerful handguns.” As opposed to less powerful handguns. Like, say, a .22 caliber pistol.
Wait! The Trace’s own graphic shows .22’s at the top of the ATF’s hit parade! And what’s up with .380’s outpacing monstrous, soul-destroying .45’s? At the same time, I’d like to make the connection between the prevalence of .40 caliber “crime guns” and the fact “fo-tays” are popularized by rappers — and the police. And while we’re at it, a 12-guage shotgun may not be a “large caliber weapon” but it’s plenty lethal. Speaking of lethality, here’s Mr. Yablon’s take . . .
All bullets have the potential to kill if they hit someone in the head, puncture a vital organ, or rip open an artery. But forensic experts say larger rounds often wreak greater havoc on human bodies. “A bigger, faster bullet penetrates further and is more likely to cause a fatal wound,” says James Gannalo, a forensic firearms consultant and former New York Police Department detective.
Peter Rhee, a former military surgeon who operated on Congresswoman Gabby Giffords after she was shot in the head with a 9mm piston in 2011, puts it this way: “A .22 will kill you, but it won’t blow your head apart.” With a higher caliber handgun, he says, “you will make bigger holes.” . . .
When bullets make impact, they flatten out. Bigger bullets have a greater diameter — a .40 caliber, for example, is about a quarter of an inch wider than a .22. That small difference could determine whether someone lives or dies, says Joseph Sakran, a trauma surgeon at Johns Hopkins Hospital . . .
It’s not just the size of the rounds that make .40-caliber pistols deadlier than smaller models — it’s that these guns are often equipped to carry more of them. Standard magazines for 9mm, .40-, and .45-caliber pistols often hold 10 or even 20 rounds.
When semiautomatic pistols can fire more bullets — because they’re equipped with large magazines — the chances that one or more bullets find the mark go up. “What I keep explaining to people is what’s important is the number of rounds on target,” says Rhee.
FYI Ms. Gifford was shot in the head — wait for it — once. And, as commentator Sam I Am points out below, Peter Rhee is saying that a .22 is just as lethal as a 9mm — only the victim’s head will be prettier in the morgue.
According to a 2014 Perelman School of Medicine at the University of Pennsylvania study, the survivability rate for gunshot wounds is around 80 percent. A fact that doesn’t see the light of day in Mr. Yablon’s piece, which highlights studies showing increased firearms-related lethality in cities where the gang bangers shoot each other with alarming regularity. And why is that?
There is some evidence to suggest that criminal shootings have become deadlier, a trend that some experts attribute to the increased caliber and magazine capacities of guns finding their way to the illicit market. A June 2016 study of 29,000 patients at the Denver Medical Center from 2000 to 2013 found that the number people admitted to the emergency room for gunshots who died from their wounds increased by six percent every two years.
Experts might also attribute some part of the increased lethality of gunshot wounds to natural selection. Gang bangers who are more accurate with their heaters live longer and shoot more people more effectively, reducing the number of less effective shooters. Making the remaining shooting population more lethal — despite increases in ER technology, efficiency and experience.
Anyway, what’s any of this got to do with legal gun owners? Shouldn’t we, the good guys, be welcoming an increase in guns with greater “stopping power”? We are! We’re buying better guns, like the new generation of pocket nines. A trend that pleases Mr. Yablon and his fellow “guys safety” advocates no end [/sarc].
One perhaps inevitable outcome of the flood of powerful handguns flowing into civilian hands is that they are showing up in sharply higher numbers at crime scenes, leading to rising fears that lethality rates — the percentage of people who die when they are shot — may be going up.
Perhaps inevitable? Rising fears about lethality rates? May be going up? As Carlos Santana sang, dance sister, dance. Dance around the fact that legal gun owners bear no responsibility for what firearms-wielding criminals use to commit illegal acts.

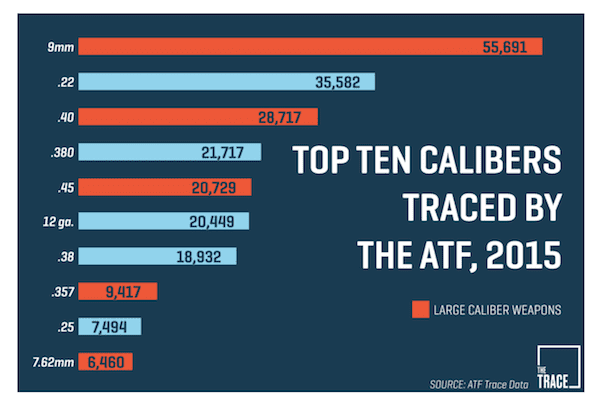



Which 7.62 I wonder?
It must be the 7.62x38R Nagant revolver. It is VERY popular among the criminal class, due to it’s compatibility with suppressors! Of course the criminals also like 7.62X25 Tokarev with it’s “armor piercing” capabilities.
Then there is the ever popular “Obrez” variant of the Mosin in 7.62X54R. That is the handgun you use, when .44 mag. just doesn’t cut it. Then, there is the Draco, and the other 7.62X39 pistol variants.
Are there pistol variants of an AR10, in 7.62X51?
Is there a Garand variant in 7.62X63?
There are just so many 7.62 pistols.
You, sir, win the Intertubez today!
Thompson Contender; they’re in rap songs constantly
PTR makes pistol versions of the G3. Sure, it’s two feet long, but if you want a 7.62 NATO handgun that’s your best bet.
I forgot about the Mauser 7.62X25, the “Han Solo” pistol.
Doesn’t matter, 7.62 is small potatoes compared to these big bore .40s, right? Hell, shoot me 3 times with a .308, just spare me from a .45 and I’ll be fine. People with no idea what they are talking about are pretty easy to spot.
At least if you get killed with a 308 you can still get into heaven…the 45 will drag you straight to the inner circles of hell.
Or worse, the .45 ACP tears a hole in the space-time continuum and drags the whole world into oblivion.
I think you’ve got it a little mixed up. Other bullets only kill the body.
45acp kills your soul.
“….drag you straight to the inner circles of hell.”
Isn’t that pretty much the description of a killed soul?
You see, that’s why we cannot have nice calibers.
Me personally? I carry a Dirty Harry .44 magum. It’s a quiet little gun that makes such a small dent that it doesn’t qualify on the ATF list of what ammmo to folllow. Well that, and the sissy criminals and rappers are chickens!t to shoot it.
Wait !!!
No .223/5.56 ???
Study must be flawed – should be at number 1
If those were outlawed, there would be no murders.
.223 rounds down to .22 and accounts for the high rating of .22…its seen simply as a distinction without a difference.
These have to be traces based on the cartridge cases left at the scene, since I have difficulty believing your average forensics expert could tell the difference between a 9mm, 380, 357, or 38 projectile, since they are all .355-358 diameter rounds. Which might help explain 38 special not having a greater showing, since it doesn’t leave casings behind at the crime scene unless you happen to reload or drop the gun.
Umm, no. There is no crime ever solved by tracing a casing left at a scene to a cartridge database. Traces by the ATF are on recovered firearms. And I think the ATF probably knows the diff between a .223 and a .22LR
ATF couldn’t find their butt if the had both hands in the back pockets of their mom jeans.
Really good at fires, explosions, and murder though.
Actually .22LR is an extremely popular cartridge with gangbangers, at least in some areas it is.
When my buddy took one to the grape at point blank the ER docs and the surgeon all told me the most common GSW’s they see are .22, .32 and .380. That might vary with region though. This was the Dayton area of Ohio.
How do they tell the difference between the .380 and 9mm? I had to ask. They generally identify it by the wound channel it creates but they also cross reference their shooting victims with police reports so they can build a database on GSWs and best practices for treating them/what weird stuff you might expect etc.
The surgeon actually said that if he could wave a magic wand and make any single caliber disappear based on his experience with GSWs it would be .22LR. Then he wondered out loud what his kids would shoot but noted that in his personal experience if there was a caliber to be eliminated “to save lives” it would be .22LR.
Didn’t know that about gangbangers; perhaps its why I still can’t find .22LR on the shelf. Anyway, the comment was an attempt at a wry explanation concerning the absence of .223/5.56mm on this list. That is all.
“GSW’s they see are .22, .32 and .380. That might vary with region though. This was the Dayton area of Ohio.”
Perhaps not the caliber but the lower cost and ability to conceal the weapon.
mk:
I suspect it’s a price issue.
The idiots in my old neighborhood swore by the Cobra .380 pistols. (http://www.thetruthaboutguns.com/2013/12/jeremy-s/gun-review-cobra-ca380-cheapest-handgun-america/) they were common enough in our area that my buddy and I referred to that gun quite specifically when we used the term “ghetto blaster”.
Then again… even Snoop Dog reps the .22:
“I got the gauge, the uzi, and my motherfuckin’ twenty-two/ So if you wanna blast, ni**a we can buck ’em/ If we stick ’em then we struck ’em, so fuck ’em!”
No 5.56? I though we needed to ban AR’s? You know, for the children!
Also 9 and .40 are now are now “large calibers”?
Side note: I want those pistols Rocket has in the new Guardians of the Galaxy trailer.
And there’s big/small difference between .38 and .357? The Trace sure knows their ammo.
.223/5.56 are less popular with bangers that 7.62 x 39 for several reasons. First, 7.62 ammo is cheaper. Second, there are a lot of cheap(ish) AKs running around. Three, an AK does not need to have a stock or a buffer tube sticking out the back like an AR, and is therefore easier to conceal.
I’m more surprised by 32ACP’s (by context with 25acp on the list) ascendance to a ‘large caliber’ despite being the second weakest common chambering
Flip the argument.
Part of our chase after bigger firepower is that our ahole neighbors who needed jobs (a/k/a: our “government”) can blast us from orbit.
Oh, mercy! Is that what I have been searching for, a handgun with which I can shoot down a satellite?
My “dream” handgun is 25mm, explosive bullet, with virtually no recoil, pistol weight unloaded no more than 24oz, 15rd capacity. None of the gun stores around here rents such, so I can’t determine how accurate I could be with it.
I keep looking.
http://warhammer40k.wikia.com/wiki/Bolter
Hits on all cylinders, with perhaps the exception of weight.
Though it is -only- a 19mm projectile… if you’re willing to compromise.
Conceal-ability is a significant downside.
19mm is not so bad. Concealed carry could be traded for an effective home defense weapon. “Real” is a serious consideration, though. We got flip phones from the original Star Trek. One day, someone may just produce the Bolter for the retail market.
The beauty of the explosive round is that you do not have to be all that accurate, horseshoes, hand grenades & 25 MM Explosive rounds!
I think the explosive 25mm rounds might really lower the need to practice, thus providing more money toward the purchase of the dream.
Now I know why all those gangs carry S&W .500’s.
“A .22 will kill you, but it won’t blow your head apart.”
It is a YUGE comfort to know that I might get dead from a .22, but at least my head will be intact…even after I am no longer interested in its condition.
It’s the difference between open and closed casket. Or don’t you want your wife, or mother or kids having a last moment with you before you go in the ground or the oven?
Always thinking of yourself.
“Always thinking of yourself.”
True, dat. You got me there.
JWM said:
“It’s the difference between open and closed casket.”
The only time someone broke into my home, the perp came into the room I was in, turned on the light, and was looking down the business end of a 12 gauge pump. I told him he had a choice: get on the floor, or have a closed casket funeral.
He chose wisely.
Darn those super strong 22LRs. Right up there with the 9mm. Boy is someones idea of powerful a bit out of joint.
50% of that list is rather substandard. But all lethal given the right placement.
Not one in the list is powerful in my opinion in any way……just adequate.
22 mag is your friend and in short barrel, a mini flame thrower.
The issue and lethality of .22 LR has to do with the fact that they are powerful enough to enter the skull but not powerful enough to exit. They just ricochet around making scrambled eggs. They do similar things in the body, and tend to tumble when they do so, so damage is nonlinear. By contrast, more powerful FMJ rounds like 9mm (the banger’s choice because they are cheaper) are typically through and through with little bullet deformation.
You heard that in a movie, didn’t you?
What in the wide, wide world of sports are you talking about?
Lemme get this straight:
A 22LR, a round that might not even penetrate both sides of an aluminum soup can at 25 yards, will deflect and still magically has enough energy to penetrate enough tissue to soup your innards?
Riiiiight…
Yay! .25 acp still makes the list! My summer shorts gun isn’t completely obsolete yet! Just a bit embarrassing though…
So ‘high capacity’ handguns are a new thing?
Browning hi-power: 13 round standard capacity, first sold in 1935
Beretta 92: 17 round standard capacity, first sold in 1975
Glock 17: 17 round standard capacity, first sold in 1982
All of these guns are older than me, and I am not exactly young anymore. But don’t let 3 minutes of research ruin your hit piece, Mr. journalist.
Dont forget Pistola con Caricato the early 1900’s 18 shot revolver.
Oh, no shit! I have never heard of that, when do we get a review?!
Went to the Gettysburg battlefield. One of the museums held several period rifles of .50, .63, and .75 caliber. I thought, “My God, what has happened to us in the mean time that we are satisfied with varmint rounds for war?”
2 things has lead to varmint rounds for use in war:
1) better powder.
2) jacketed bullets.
The simple answer is we use them because it’s enough. It’s usually enough to take the enemy out of the fight. Sure, there’s anectdotes of persons hit by multiple 5.56 rounds and continue to fight; There’s also anecdotes of persons hit by RPG’s who continued fighting.
Enough is just that…and more is better (caliber wars)
Wondering what the ISIS, et.al. response would be if they found us using those Civil War calibers in modern bullets? Heck, how would the Wehrmacht have responded?
A Army surgeon once told me that the .58 caliber Minie Ball was the most devastating round ever used by the US military. The only difference between today and 1863 is that the amputee would survive the amputation.
To expand on what Chris said, with the advent of smokeless powder and high velocity rounds, it was discovered that lead bullets performed very poorly. The rifling would strip off the outer layer, thus imparting little rotation reducing accuracy, and fouling the barrel. Further, lead bullets were outlawed and fully jacketed rounds were required for warfare to minimize the hideous wounds caused by the impact of lower velocity lead rounds that pancaked on impact.
Yes, understand the issue with lead bullets of the time. It is the caliber that was impressive (whether lead, stone, concrete or jacketed). .75 caliber?
Interestingly, men of those days were willing to march in dressed ranks into massed fire of rifles of those “large caliber” bullets/balls. Wonder if fighters of any army would be so wiling today?
Sam, remember that at the time of the civil war most army’s in the world, including ours, had punishments that included flogging for not obeying orders. Also, being branded a coward had all sorts of repercussions for the soldier, up to and including execution.
And in the Union army of the civil war most of the troops were not regulars. They were men that enlisted into regiments that were raised locally. You served with neighbors and family from the same community. Any misbehavior on your part would lead to repercussions that lasted long after your service was over.
The 18 shot Petersen Pepperbox existed at least as early as the early 1840’s. There may have been “high cap” ones back further considering the Pepperbox has been around since the 1400’s.
Okay, they got me. I’m the reason that Chicago gangsters have better guns than they did back in the day of Al Capone. Me, in Massachusetts. Mea culpa. Mea maxima culpa.
Now what?
If only gangsters could just go back to using those underpowered .45 ACP full auto Tommy guns like they had in the ’20’s, the streets would be so much safer.
Don’t forget the short barreled 10 gauge shotguns, like the one that got Mr. Miller in trouble.
God bless the CNC machine and the 20 year old programing and running it.
The only “high caliber” handgun round I see on there is .357 Magnum, unless we’re just calling everything above a 22 high caliber now. And .357 is below 12 gauge. So I’m not sure if this says what the author wants to see it saying.
This is really so simple, a caveman can understand it.
As more guns of a caliber above .173 are bought, more become available for loss and theft. As more of these blasters above .173 are lost or stolen, more are available for use in committing crime. Who are the initial purchasers of these devastating calibers? Law-abiding people. Ergo, as the inventory of guns .174 and greater increases, the more the likelihood of use in crime increases, all due to the increase in legal purchases.
Like this: The more we have expensive cars purchased by law-abiding people, the greater the likelihood these expensive cars will be involved in accidents and/or stolen. This means that more of these expensive cars are pushed through chop shops, and their parts illegally sold. Another example of law-abiding people contributing to a rise in crime.
Criminals do not make themselves criminals. Criminals are made because they were mistreated by non-criminals, somewhere, sometime, somehow. It is just plain, unjustified, unwarranted unfairness.
Absolutely correct. We should correct this horrible abuse by killing them all and forgetting they ever existed. OK, right!?
Hi Larry.
Stand a little taller, and read it again.
I think a better correlation would be price per round.
That, sir, is an excellent point.
25 caliber? Really?!? I’m throwing out a big BS…and those fed boyz have the lowly 22 in 2nd. I’m right there with the 9mm and the 12gauge?
Uh, I’m not the expert, but isn’t there a .25-06?
.25-06 is a rifle round & moderately uncommon.
There’s also a .25 acp; not exactly a commonly used round. But would be concealable unlike a 22inch barreled .25-06.
Uh, caliber = bore size, right? Which means 9mm and .380 are the same caliber .355 in) and .357 and .38 are the same caliber (.357 in). Their damn ranking makes no sense. Hell, a twelve gauge Issa HUGE caliber. Maybe they mean high power? Hard to tell with props as they are confused so easily by facts.
Personally I consider .357 magnum a high powered handgun, but only minimally so. Real power starts at the .44 magnum, which is as much dynamite as want to hold in my hand when it goes off.
I’d say the .41 mag, but otherwise agree.
Eh, not much difference between .410 and .429.
I feel stupider reading that article.
It explains in no uncertain terms what “caliber” means, yet this obnoxious graphic self-contradicts the explanation.
9mm (.355 inches) is “large caliber” (don’t look at .380… same size projectile is not)
BUT
.38 (.357 inches) is not
BUT
.357 (.357 inches) IS
BUT
12 gauge (.729 inches) is NOT
BUT
7.62 (.308 inches) IS
Don’t forget the deadly “9mm piston” (sic) The Trace refers to.
An integral part of the 3 cubic inch V-8.
Don’t forget, the guy who wrote this did not have a *CLUE* what he was talking about!
Exactly!! You hit the nail on the head PeterW. Also, a .729 caliber (12 guage 2-3/4 inch casing) one ounce slug traveling at 1300fps (same speed as a 9mm) will go through both front shoulders of a large white tail Buck at 100yds. Been there done that. Oh, but it’s a small caliber. LMAO!
Glad someone else caught the “large caliber” nonsense. I’ve personally never heard of any large caliber in anything other than a rifle. Maybe .762/308 counts but that’s at the very start of large caliber IMO.
Don’t mean to start the caliber wars here, but I heard someone say something about the lethality rate for 9, .40 and .45 being less than 1% different. That being said, I have no sources, nor can I even remember where I read this.
I’ve seen similar numbers based on comparisons of police one-shot stops (not necessarily kills).
I remember seeing a chart that said 12 gauge buckshot, .357, and .40S&W were the top one-shot-stoppers, but I think that’s more like because they are the most commonly used rounds by cops that actually use their weapons, whereas 9×19 is the most common round around the world but mostly stays holstered in the “civilized” parts of the world.
You are thinking of research done by Massad Ayoob. He lays out why .40, 9mm and .45 are virtually identical in terms of lethality. Very good stuff. Basically when you are looking at handgun calibers there isn’t as big a difference in lethality as there is in rifle calibers. Which may seem obvious, but seeing how many survive all handgun rounds compared to rifle rounds is pretty amazing considering they all perforate something not very well suited to perforation. Of course bullet design plays a big factor in energy transfer and there’s tons of other variables. But really helpful information I think. I chose 9mm over .40 and .45 back when I first read his stuff because you can stuff more rounds in a similar sized gat.
Unless gangsters are shooting each other with old Swedish moose rifles, I think they need to re-evaluate their description of 9mm as a large caliber. And I’m pretty sure they aren’t, given that I haven’t heard a lot of references to potatiskastaren in popular hip-hop.
Maybe they are using them, but it’s just really hard to rhyme with “potatiskastaren”.
So what? Toyota Corollas are probably involved in more lethal accidents and hit-&-runs compared to other models, but all that means is that a lot of people are driving them.
What measurement of caliber size has a 9mm above a 12g?
Diameter? Nope, .355″ < .73".
Muzzle energy? HELL NO. 500-600J << 4000+J.
Probability of getting the gun ignorant to think they're too powerful for civilian ownership? Maybe.
It says a lot about their audience when they fail at basic math and can’t even convert inches to metric, yet they can get away with crap like this.
“a .40 caliber, for example, is about a quarter of an inch wider than a .22.”
Hmm. Well, .40 – .22 = .18.
A quarter of an inch = .25.
Close enough for morons!
“Hmm. Well, .40 – .22 = .18”
Which model calculator?
Twenty or thirty years ago, Richard Davis of Second Chance Body Armor “fame” (the guy who used to shoot himself while wearing his product) made the argument in one of the videos he used to put out that criminals went to more powerful handguns because of the dwindling number of “saturday night specials”, i.e., cheap-cheap, crappy little small caliber handguns. The numbers were dwindling because they were basically mostly regulated out of bidness. The video was called Second Chance vs Magnum Force. Probably out there on YouTube.
The thing that concerns me the most about The Trace is that by implication the people who read it and believe it are by definition more ignorant than even the folks who write the rag.
That almost makes me want to advocate for mandatory firearms training in schools… but then no doubt some of these morons would apply for the teaching positions!
This difference in caliber between .380 and 9mm is 0.01 mm. Pack of damn idiots, these people.
The numbers (and facts) are completely irrelevant to these folks. Most of the time they just make random crap up. It’s the emotional appeal they are going for, so they just say anything they think will scare those folks who don’t know anything about guns, crime, life, etc (their target audience).
Actually, both .380 ACP and 9mm Luger use bullets that are 0.355 inches in diameter.
Under their theory that diameter is king, the 0.355″ diameter bullet from a .380 ACP is nearly as deadly as the 0.357″ bullet from a .357 magnum. Whoodathunk?
So we’ve addressed the ATF. Pardon the aside, but this warehouse fire in SF keeps referring to the ATF, even once referring to them as “Alcohol, Tobacco, and Fire” being involved in the investigation, am I the only one who wonders WTF? Organization needs to be closed.
I’ve often heard them referred to, in derogatory terms, as the Bureau of Alcohol, Tobacco, Firearms, Explosives, and Really Big Fires.
I think that magazine capacity limits result in larger calibers. I lived in a state that had a ten round limit and I seemed to always default to .45 rather than something smaller. If I could have a magazine with 17 rounds of 9mm, I probably would have bought that. In fact the last gun I bought (now living in Utah) was exactly that.
Eh, I’ll take a 17-round mag of .45 over a 17-round mag of 9mm if I can. Baseplates ain’t cheap, though.
solution is easy.
just carry 10mm. ammo isnt cheap and the guns aren’t plentiful or cheap like Hi-Point sh!t
So a 9mm and a .357 are “large caliber” while .380 and .38 are not……
Somebody doesn’t know what “caliber” means.
Or “gauge”, for that matter.
I don’t see the .9mm on that list.
Rimshot, please!
That was good. Really good.
Wait wait wait.
9mm, 40, and 45 are large caliber weapons, but 12ga isn’t?
“A .22 will kill you, but it won’t blow your head apart.”
I am sure your undertaker will appreciate the difference.
That little gem came from the surgeon who operated on Gabby Giffords who, ironically, was shot by a 9mm but it did not kill her.
I know both Drs. Rhee and Lemole. The neurosurgeon operated on her, the trauma surgeon managed her care.
On a side note, I believe Dr Rhee still takes his residents out to the range once a year. And most trauma GSW’s can be ‘broadly’ categorized into handgun (all calibers)<rifle(almost all calibers)<.50 cal (military only in reality). Shotguns are a matter of distance. Again, these are generalizations but reasonable ones. Many trauma/ER docs have lecture slides that seem to follow this theme (including Peter Rhees :P).
The crime scene clean up crew will certainly appreciate it.
Curious that The Trace considers 9 mm to be a “large caliber” but not .38 or 12 gauge and they don’t even mention .223/5.56. Oh well. What can you expect from people who are incompetent on the subject of firearms?
I think what’s being forgotten here isn’t that the graphic shows lethality, but the number of guns traced, by caliber.
Thus the difference between, say, .38 and .357. More .38s were traced than .357s.
And, as well, the word “caliber” has different meanings; to the uninformed, “caliber” equates to a fear factor; the higher the “caliber,” the more fear is experienced.
To the informed, “caliber” refers to the bore diameter.
Thus, to us (I’m assuming us to be at least somewhat informed), a 12 gauge shotgun is indeed a large caliber, while to the hoplophobes it’s a non starter since it’s used to hunt rabbits and quail, and therefore not perceived as a threat.
Looked at that way, the graphic makes a lot of sense.
The real winner here is 10mm: So powerful it does not leave a trace of evidence!!
“According to a 2014 Perelman School of Medicine at the University of Pennsylvania study, the survivability rate for gunshot wounds is around 80 percent.”
The current state of marksmanship in this country is a disgrace…
According to the TV show Chicago PD .22 lr is know as the “assassin’s bullet”.
Really? I thought .22 was the Redneck-Tincan Special.
Only when it’s made of ice.
12ga is not?
SAY WHAAAAT?
12 gauge is not large caliber? Do tell.
I was thinking the same thing! 9mm is labeled as “large caliber” but 12 gauge and .380 are not labled as such. The stupid is strong with this one.
“12 gauge is not large caliber?”
Maybe a slug, but generally, the pellets are not larger than .33 caliber (if I remember some article correctly). Of course, it would be amazing if the author of the chart actually understood the difference between slug and pellet.
Christ
I’d much rather be shot with a 9mm than a 12 Guage lol
Man, even .25 ACP beats out any .32, be it ACP or a .32 revolver cartridge. I guess we can put the .32 to rest then.
.32 caliber handguns
1860-2016
You had a good run, baby. Gone, but not forgotten.
Interesting spread on the calibers in the chart. Otherwise, used by an obviously ill-informed writer, who likely does not care one bit about factual accuracy because he/she only intended to use the ATF’s (“credible” Government Source to the worshippers of the State) findings to create “scare propaganda” to terrify the liberal-mindless proles and “prove once again” the inherent evilness and danger firearms pose to them. Better to be robbed, raped and/or murdered than to risk providing for your own self-defense or fighting back, which is too dangerous for the common schlepper to attempt. Another crock of libtard word scatology to be devoured gratefully by the Serfs and rejected completely by those of us who actually value our lives and those of the people we care about.
I think that the guy must have seen 12 ga., and figured that it was such a small number that it must be small caliber. Or, something like that. Must think that 10 ga. and 8 ga. are even smaller caliber. Which is where most everyone knew for sure that the article to be complete BS. Figured something was screwy on the first entry (9 mm as large caliber) after all the debate over the years in the caliber wars (which this author obviously missed), but esp. as the FBI moved from 10 mm to .40, and now to 9 mm for the ladies.
Criminals are using larger calibers? Do you remember when you campaigned against “Saturday Night Specials”? Of course you don’t. Do you remember when you campaigned for magazine capacity limits? What did you think people were going to do, walk around with a big empty space in the grip? Maybe keep their contact lenses in there?
If you follow the article’s sources back, you’ll see that these were firearms recovered at a crime scene. They are not necessarily firearms used in a crime. If a woman stabbed a man in his house, and they recovered an unfired Colt Python in a locked case on the floor, that .357 would get included in the chart. If someone shot me with a Glock 17 while I was in my truck, that chart would add another 9mm, as well as the 7.62, 12g, .45, and the 9mms of mine, even if they were not used in the crime itself.
What the hell does “traced by the ATF” even mean?
So lets see:
1. The top “large caliber” is 9mm which half of the keyboard commando will tell you is dangerously under-powered
2. It lists 12ga. Where do I get a 12ga handgun?
3. It doesn’t list 12 ga as a “large caliber” WTF?
4. So my thirst for bigger caliber hand gun led Georg Luger to invent the 9mm round in 1901? Is that what I am supposed to get from this?
Hearing RF actually say/sing “fo-tay” would make my Christmas 🙂
Didn’t I just read here or at Breitbart about an elderly male homeowner who dispatched a home invasion suspect with ONE shot from his, the homeowners, never before fired 30+ year old .22 caliber revolver and 30+ year old ammo? Proof once again Bloom-BOIG’S propagandists know NOTHING about firearms or ballistics. I can’t tell you how many criminal gene bearing “urbanites” engaging in violent behavior have been “made good” by a “little” .22 or .25 “pinballing” and tumbling around their torso ricocheting off vertebrae, ribs, and other bones turning their vital organs to mush where a larger caliber round would pass right through.
This article is written by a man of dubious credentials: http://observer.com/2014/12/how-the-72-million-kid-duped-new-york-magazine/
“Standard magazines for 9mm, .40-, and .45-caliber pistols often hold 10 or even 20 rounds.”
I would like to know where I can buy a .45 with standard magazine capacity of 20 rounds. Also, I would like to see if I can get my hand around it before I purchase…
Interesting how .38 (Special) and .380 (ACP) are not “large caliber” but 9mm (Parabellum) and .357 (Magnum) are.
As I said before, “caliber” and “power” mean about the same thing to hoplophobes, because they are ignorant when it comes to firearms. Details (like facts) don’t matter, because, quite simply, all guns are bad, so why sweat the details?
The buyer wishes
Comments are closed.