“An anti-violence organization recorded 52 anti-LGBTQ homicides in the U.S. in 2017,” an email blast from The Trace reports, “the most it’s ever recorded in a single year. 53 percent of the victims were killed with guns.” Hey! Not “by” guns! Well done Bloombergians! And if you think about it . . .
53 percent is just over half. A fact — if a fact it is — that indicates that the LGBTQ community needs to pay attention to something other than guns. In terms of threats headed in their direction, I mean. In terms of countering a threat, they should pay a lot of attention to guns. As in tooling-up.
Clicking over to the report by the anti-violence org in question — the National Coalition of Anti-Violence Programs (NCAVP) — we learn that the study calls the LGBTQ people shot and killed in 2017 victims of “hate violence homicide.”
We also learn that police shot and killed three of the firearms-related LGBTQ homicides cited. Are we to assume that those police shootings were motivated by “hate violence”? A citation would help there . . .
The NCAVP study also reveals that 32 percent of victims knew their killer. Again, do we know for sure that the killer murdered their victim because they were LGBTQ? I mean, that is the point of this report, yes?
You and I know it’s not the means that’s important. It’s the murderer’s intent.
More than that, we know that all Americans have a natural, civil and Constitutionally protected right to keep and bear arms. We The People of the Gun lament the loss of any innocent life, regardless of race, color, creed or sexual orientation. We encourage all LGBTQ self-identifiers to exercise their gun rights in their own defense. That is all.

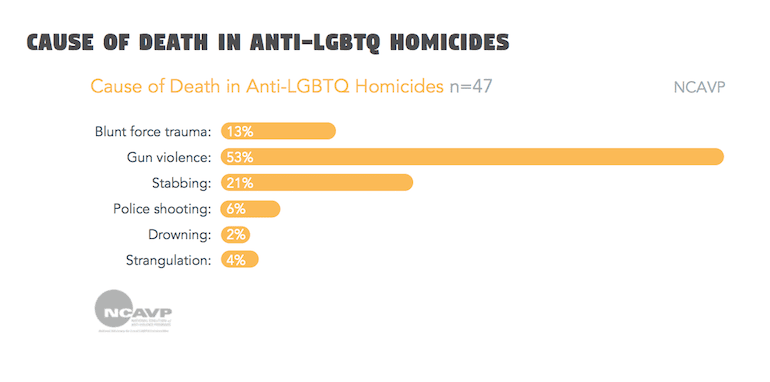



This is the latest attempt by Big Gay to push their sgenda. Most of these homicides were gay on gay. Case in point. The first anti-LGBT “hate homicide” in 2018 wad tranny killed by its husband.
Although no one likes to acknowledge it, LGBTs, broadly speaking, have a wildly disproportionate propensity for suicide, as well.
Really? Go figure…
Dunno about gays and lesbians, but 40% of transsexual people kill themselves AFTER they’ve had their sex-change surgery. I always discourage my trans friends from getting surgery, because having a literal gaping axe-wound or a balloon-dick is not something anyone really wants to have. Psychiatrists and surgeons will tell you anything and do anything to you to get money out of you, and they really don’t care about anything but the money.
Oh bullshit. Just because someone was murdered happened to be gay doesn’t make it anti gay violence. Perhaps the murderer was also gay, making it gay on gay violence. Just more fake news.
Lesbians have a high rate of domestic violence in their relationships, much more than straight couples, and much, much more than gay guys. Bitches be crazy.
Lesbians have a much higher rate of domestic violence in their relationships than straight couples do, and a much, much higher rate than gay guys do. No one wants to talk about that, though.
Have you got a link/cite for the domestic violence info? I’d like to read more on that.
I don’t have a link or a source, but I’ve heard it from places I tend to believe. (That’s generally how my mind classifies things, trusted source/not trusted source. I often don’t remember the specific source).
I have the same memory problem. My sister once told me that if I could just remember the sources of all the facts I knew I could be rich as a consultant.
Alas…..
Yeah. The “I don’t remember the case name, but that’s definitely the law” doesn’t fly in court.
Well, women are more violent then men. It’s just that men are a hell of a lot tougher and can usually take it and survive.
As Kipling put it, “… the female of the species is more deadly than the male.”
As Jonathon Rauch said in Salon magaqzine in March of 2000:
“Thirty-one* states allow all qualified citizens to carry concealed weapons. In those states, homosexuals should embark on organized efforts to become comfortable with guns, learn to use them safely and carry them. They should set up Pink Pistols task forces, sponsor shooting courses and help homosexuals get licensed to carry. And they should do it in a way that gets as much publicity as possible. ”
*the number is now over 40
We must end this Ze on Zer violence!
Not my circus.
Not my monkeys.
Not my problem.
Or said another way….
So what?
I suppose one could also say all domestic violence is, technically, hate violence. As opposed to friendly violence.
I suspect that a good portion of “friendly violence” is “domestic.”
Hey, whatever works. Just please not out in the street where it scares the horses.
Considering that about 66%* of all homicides are firearm-related, it’s interesting that this subgroup has a rate that’s 10 percentage points lower.
*That’s from memory. If that’s wrong; please correct me.
Yes, that’s what I thought. 53% means a lower percentage are killed using guns.
Since most homicides are gang violence and I’m thinking “out of the closet” LGBTQ are less common in gangs. Plus I would expect most actual hate crime is a bit more personal than using a firearm. So I’m not really surprised the percentage is lower. Also as pointed out above most of the gun related violence is likely domestic.
N=47
N=32
Don’t get me wrong, that’s technically okay for statistical analysis, if you were actually doing analysis (this isn’t). But examining 30-50 people isn’t really that big of a sample size as far as human populations go. But if you were to do analysis, you could use the data to compare to national data to see if there is a significant difference in rates.
LGBTQIA people aren’t actually a very large group, despite what Democrats want you to think.
I’m not reading a nonsense study where a conservative estimate would put the number of murders at over 64% sexual deviants,* and the study calls it “hate violence homicide,” so I can’t say, but this sample could be all the sexual deviants who were murdered.
*I use the term sexual deviants because it is accurate. These people’s sexual behavior deviates from the normal, I think queer would probably be considered more offensive, and I’m not using the continually changing alphabets soup derivative that now includes queer. When I was a boy, queer just meant homosexual, while gay meant homosexual or lame.
53% is an interesting statistic. The most recent FBI crime report shows that firearms are used in 73% of all homicides. So what caused this 20% difference?
Probably because they are more likely to be personally motivated killings rather than, say, drive-by shootings due to gang violence. Romantic partners killing each other tend to be more likely to use whatever is at hand than the biggest purveyors of violence in places like Chicago and Baltimore.
I’d also suspect that LGBQTetc- a disproportinate amount of whom probably live in urban areas- are less predisposed to have a gun at hand than, say a old white dude in rural Kentucky.
Historically, the most common cause of homicide among gays is Anally Injected Death Serum. Since 1985, everyone on the planet has known how AIDS is spread so all those deaths from it are either homicide or suicide. Knowingly spreading AIDS is assault to commit murder and/or murder.
Except in California.
Or PERHAPS just classify it as suicide.
Regarding the current media fetish with “trans” – What it the difference between “gay” and “trans”? Both are all about crazy and dick in ass.
Putting police shootings as a seperate line item is interesting. I suspect this group does not know the difference between murder and justifiable homicide.
Then again, live with the Village People…
This also caught my eye. So the police are specifically targeting the LGBTQIA community, I thought we were over this after Stonewall?
Only 52 out of a total population of what, a couple million? Ten million, maybe? Sounds like they’re pretty safe overall, then.
The intolerant, anti civil rights bigots have used up just about all of their smears and slanders in the vain hope that something, anything would stick. They have labeled us as being racist, misogynistic, homophobic, transphobic, baby killing Putin puppets. (Repeat that last sentence three times, as quickly as you can.) They are reduced to riding the coat tails of the snot-nosed idiot children our universities are pampering, in their pathetic attempts to remain relevant. Forming alliances with minuscule, extremist fringe groups composed of undisciplined brats who are acting out is an indication of sheer desperation.
50% is far less than the national average. The reality is that the gaystapo will never admit that the vast majority of this is caused by the behavior of their own community.
If you actually read the accounts of the killings in the linked file you find that very nearly none of them were likely killed due to being LGBTQ. A few sure and a few more maybe.
Most are run of the mill domestic fights, robberies gone wrong, unsolved murders that took place in places where no right thinking person should be (hence there isn’t even a suspected motive) or killings linked to online dating apps. One guy killed in jail was very likely killed for being gay and another guy got himself shot for sticking up for his friends who where also LGBTQ. Few have much to do specifically with “LGBTQ hate”. In fact the dating app killings were probably either set-ups by sickos/robbers or fights that resulted in LGBTQ on LGBTQ violence (dates gone very bad).
As such the whole thing is pretty much pure bullshit.
I’m sure the Trace would be ecstatic if gay people would start stabbing one another to death exclusively instead.
100% of homicide is caused by murder. See, I can statistics too!
You got it backwards, 100% of murder is caused by homicide. So by just getting backwards instead of so very, very wrong, you statisticed to well to be comparable.
If You choose to undertake a dangerous and deviate forms of lifestyles…Then the problem is on you..(Re: This was part of past Law Enforcement investigations, research, and LE SOP…In many states, before they all went left-wing STASI…I remember at the Hospital PD that one of my relatives worked for had similar LE news flash, BOLOS , SOPs and other facts related to this type of stuff…Then it all went PC overboard, and the PD department memos, etc… Changed, like a memo I saw that targeted *white* males, libertarian, or NRA types…That warned that these catogory of people would most likely be armed, and carry a sovereign citizen attitude…That these people should be considered dangerous…) Boy, how times have changed…1984 is just a little late…..
Homosexuals have a right to self-defense just like everyone else.
Most homosexuals don’t understand this because most homosexuals are socialist progressive in their political orientation.
Gays need the government to force their agenda on the rest of society. That is why there is NO elected homosexual who supports the Bill of Rights.
I think a split occurred when so many gays came out to support Donald Trump. Milo had a lot to do with this. Now there are more than just the Log Cabin Republicans, Tammy Bruce, and the Gay Patriot blog, who support Liberty in the gay community.
Homosexuals as a group have a long way to go to accepting the concept of Liberty.
So we have gun violence on the chart, but no water violence, fist violence, cop violence or stranger violence. Yup, no bias here…
Also people get murdered for a variety of reasons. The ‘I killed them because I hate all people like that’ is fairly rare.
Drowning?
Protect your labor day festivities: Just say NO to LGBBQ-related homicide!
Every time i see a bullsh!t article from the trace, i wonder how that many villages can lose their idiots.
Isn’t the general homicide rate higher than 53% firearm related?
That would mean if you’re LGBT you’re less likely to be murdered with a firearm than a random crime victim.
if I were going to murder I would use a gun, because it is efficient. People murdering without guns are either over-achievers or stupid.
Maybe that’s why the majority of murders were committed with guns?
I’d probably go the over achiever angle if I wanted to get away with it. I might not if I had a bunch of cheap Taurus revolvers that I happened upon.
“We The People of the Gun lament the loss of any innocent life, regardless of race, color, creed or sexual orientation. ”
I’m so glad you clarified that by saying, “innocent life.”
Chicago, per https://heyjackass.com/ has 89% of homicide victims dying by gunfire.
In other news, water is wet. And criminals ignore our laws.
And last, but not least, the only thing that stops a bad person with evil in their heart is a good guy with a gun.
Isn’t the far more provocative story here how 10 or so homosexuals were freaking beaten to death? I mean, I get it. Bloomberg will always try to make an anti-gun interpretation, but holy crap, shouldn’t a savage beating be held in special regard?
“We The People of the Gun lament the loss of any innocent life, regardless of race, color, creed or sexual orientation.” Lament: “a passionate expression of grief or sorrow.” My monkey brain (see monkeysphere) doesn’t have the capacity to lament the death of most people, and I’m honest enough to admit it.
“We encourage all [] to exercise their gun rights in their own defense.” That’s better.
Comments are closed.