“The 600 Casualties From One Of The Deadliest Mass Shootings In US History Made Us Rethink Our Coverage,” Lemonade insurance CEO & Co-founder of Lemonade insurance Bob Schreiber writes on the company’s website. And so he’s published the following manifesto statement:
‘Guns’ is a polarizing topic, which is why most companies avoid it at all costs. But Lemonade was founded to make insurance into a social good. That requires being upfront about what we think ‘good’ is, and is not. When it comes to the Second Amendment, therefore, we can’t take the Fifth. After the awful massacre in Las Vegas, we’re not sure anyone should.
Our company, like our community, includes gun owners as well as gun control advocates. Many are both. But while we respect gun ownership, we’re not into gun worship.
This is why our policies limit the amount we will pay out for the damage or theft of firearms to an entirely adequate $2,500. If you own more than $2,500-worth of firearms, we recommend trying one of our competitors. They seem to all offer additional coverage. We don’t.
Our policy already excludes coverage for any illegal guns or gun use, but in our next version we plan to add more protections around firearms:
1. We will exclude assault rifles altogether. We simply don’t understand why civilians need military-grade weapons, and we prefer not to insure them.
2. We will add requirements that firearms be stored securely and used responsibly, upon penalty of voiding coverage. We believe guns should be treated mindfully and soberly, not as a plaything, a status symbol or an ideological prop. Reasonable people, we believe, can agree on that.
As an insurance company, it falls to us to shield our customers from damage to their guns, and by their guns. It stands to reason that we want members who take the responsibilities of gun ownership as seriously as we do. And so, we’ll continue crafting our policies for the vigilant gun owner, not the vigilante gun owner. The former are welcome, and will find our policies cover them fully; the latter aren’t, and won’t.
We’re under no illusion that our industry, let alone our company, can solve gun violence. But being unable to change much doesn’t give us license to change nothing. Here’s to everyone doing their part.
Postscript: As a company built on transparency and trust, we plan to broach politically and ethically charged topics periodically, and to be open about our efforts to align our investment practices and insurance policies, with our best sense of what’s the right thing to do. This is post #1 in our new ‘Ethics of Insurance’ series.





I don’t have a problem with that…they can market all of the insurance that I’m not going to buy all they want to.
Bingo.
They have the right to be anti-gun and you and I have the right to be anti-lemonade.
They sink or swim based on their products/service. If they resonate with a segment of the market then they’ll probably stay in business, if they alienate a large enough segment, well then they may find themselves out of business.
“If you own more than $2,500-worth of firearms, we recommend trying one of our competitors.”
Based on that statement alone I’m guessing a lot of gun owners will be steering clear of them.
I see nothing in the 2nd amendment that implies that it only applies to government. After all, the 13th exclusively does not.
Are you suggesting that this company limiting their insurance coverage of guns against theft is infringing your right to keep and bear arms?
Yup. I define the term “infringe” very broadly. The fact that their actions are specifically targeted at gun owners rather than owners of other dangerous high-value property makes them inherently discriminatory. We’ll never win if we don’t make the enemy play by their own rules.
There is no right to buy insurance, and no duty on the part of a private company to sell it to you. And, if you do buy it, you are promising to abide by the rules of the contractual relationship.
Limiting coverage on insurance is hardly an infringement – try buying motorcycle insurance as a 20 year old sometime.
I wholeheartedly disagree with these guys, however, they should have the right to provide or refuse service; just as I think a bakery should have the right to deny service to a couple who wants a pornographic wedding cake, despite their membership in a protected class.
But in the meantime Lemonade should be forced to provide service just like the baker, florist, and photographer.
When the baker, florist, and photographer get their liberty back then so can Lemondae.
In the meantime what is forced on the Right, should be forced on the Left.
Actually, the 13th amendment, like every other one, only applies to the governments. In this case, it amends the Constitution to abolish slavery (immediately invalidating all federal, state, and local laws about the slave trade, runaway slaves, etc.) and give Congress the legislative authority to enforce that abolition, presumably by punishing those who engage in slavery. If you attempted to engage in slavery today, they wouldn’t charge you with violating the 13th amendment, they’d charge you with violating the laws Congress passed using the power granted by the 13th amendment.
The Constitution exists as a compact among sovereign states (not people) to set up a common federal government. So, by definition, it only applies to the federal, state, and local governments. If I broke into your house and gathered evidence that you were engaged in some criminal activity, I could give that information to the DA, they could use it in court against you, even though I didn’t have a warrant, and I could never be charged with violating your 4th amendment rights (but I could be charged with burglary).
By your “logic”, I couldn’t tune you out for being an idiot, because it would violate your right to free speech, nor could I kick you out of my house for being an armed idiot.
Actually, the 13th Amendment does not forbid slavery and forced servitude. What is says is that they are forbidden unless used as punishment for a crime. No mention is made of how serious that crime has to be before you can be punished for it by being declared property of the state.
I’m really surprised the socialists haven’t tried to use this, but then none of them have ever bothered to actually read the Constitution. And after I finally sat down and read it through and noticed this, I’m convinced most of us on the right have never really read it either.
Then the government can come in and require you purchase it like with health insurance.
Sure as long as the Government require Everybody to get it and not just gun owners.
In the end the policy holders will end up buying guns just to get the price break for costing the insurance company less for having it.
“1. We will exclude assault rifles altogether.”
If we have that in writting, well hold them to it: my AR15 is not an assault rifle. My Mini14 is not an assault rifle. My 10/22 – despite its current appearance- is not an assault rifle. My SKS is not an assault rifle.
If they insured someone like me and refused to cover such firearms I’d say I had a good claim that they were in breech of contract and could sue the crap out of them.
What they are doing seems little different from any insurer from a few decades ago who would have refused service to black people – and for much the same reason.
It would depend on their definition of ‘assault rifle’. If they fail to define the term in the policy (contract) I’d guess you’d have a claim, based on the common and accepted meaning of ‘assault rifle’: …capable of selecting between semi and fully automatic fire.
The precedent on set in that challenge to the legal meaning of the term ‘assault rifle could have far reaching consequences I would think, but I’m not a lawyer.
Excluding “Assault Rifles” would require a definition of an assault rifle. Assault is an action, not a device. You can be assaulted by someone with an AR-15, a baseball bat or a claw hammer, among a multitude of items.
Is there any manufacturer of firearms that classify any of their products as an “Assault Rifle”?
An insurance policy can include or exclude any item or policy holder action, as long as all parties are aware of and agree to the inclusions and exclusions.
Actually the military designates their smaller rifle caliber select-fire battle rifles as “Assault Rifles” (like the M-16) so if you get a large bore select-fire battle rifle you should be fine.
Once it is legal to buy them anyway.
Bullshit. This has nothing to do with being a good company, and everything to do with denying coverage for otherwise insurable losses, or limiting what they have to pay on claims. Do you think they will cut their premiums accordingly? Of course not. They want to punish gun owners, so they will charge as much as possible and pay as little as required.
The ethical insurance company would provide increased coverage for insurable losses that involve guns, especially under liability polices designed to compensate those hurt due to negligence. They would offer premium discounts to gun owners who show that they lock up their guns when not in use, or who prove that they have taken classes on safe gun storage.
This is horseshit masquerading as a hot dog.
In my experience, there is no such thing as an “ethical insurance company”.
No, this has everything do with the company being a bunch of douchebag Leftists.
Who cares what Lemonade insurance does. They are irrelevant. Do you hear me Lemonade? Irrelevant.
To make Leftists follow the same rules that they make us follow….
I insist that Lemonade provide their service and ensure my 20K$ gun collection if I was so lucky to have one.
Why am I not afforded equal protection under the law?
If the baker, florist, and photographer have to provide their services to every kind of event they don’t like then why doesn’t Lemonade have to provide their service in areas they don’t like?
The Right very rarely fights back. We just keep bending over.
We unfortunately have very few true conservatives that want to spend their money to make a difference.
Their company, their product. They can create any type of policy they want with any number of exclusions. If you don’t like it, don’t buy the coverage. At least they are being upfront about it; hows the old saying go, if life gives you lemons, make lemonade! But seriously, there are plenty of options for coverage so lets move on.
Nope.
Just like the gay couple that insisted on the cake from a particular baker I want my 20K$ worth of insurance from Lemonade.
I’m tired of the Left not having to play by their own rules.
Free market in action (I bet Lemonade would be embarrassed to know that). Good for them.
I do wish, however, that we could have one single arena of American life that didn’t become a political battleground.
Then this wouldn’t be the USA.
+++XB=3~<
Thanks to the Left (and also the Right) the government has grown to the point where the government is the primary decider of who wins or loses.
When that happens, every aspect of life becomes political.
Groan.
The bigger the government the smaller the citizen.
If I ever need insurance for my lemonade, I’ll give them a call.
Oh wait. No I won’t.
$2500? So if I own a colt snake gun, I’m screwed?
Or a Cabot?
Or a les Baer?
Or any nice rifle, shotgun, and pistol?
I know fudds with more tied up in hardware than that.
I wouldn’t be able to decide which of my guns I’d have them insure. So, I won’t have them insure any. I’ll be very glad to do 100% of my business with their competitors.
LOL!! Okay then. You don’t want me as a customer and I don’t want you as my insurer. Free markets at work!
I wonder if they have ever looked at the prices of guns and realised 1 or 2 higher end over unders or decent hunting rifles with scopes can easily top $2500.
They do not care how much guns cost, they want you to not have guns. The incentive is that Lemonade provides almost no reimbursement for loss of your guns. The idea is that Lemonade gets a button for being a proud member of the anti-gun mafia, maybe you get rid of your guns so you can buy their insurance, or maybe they just rid themselves of another deplorable.
considering their AR spiel, i’d say it’s safe to assume they have never heard of an O/U let alone what they cost.
Wasn’t gonna buy their insurance anyway… I already have home owners that covers my guns up to their full market value.
Never heard of them, so this is clearly an advertising stunt mixed with virtue signaling.
Exactly
Agreed, but with just a sprinkling of rear end covering. Hence the obligatory “We support the Second Amendment, but…..” bit and the useless token $2,500 coverage limit. They’re anti gun, always have been, and are using this event finally as an excuse to act. They just want to avoid any blowback in the process.
I’m in the insurance biz — this is all virtue signaling. Lemonade’s target demographic is urban millennials that probably don’t own $2,500 of anything that requires a separate endorsement/rider.
Almost no homeowner with real assets, a couple cars, and a “toy” or two is looking at Lemonade at all.
Nailed it. I was about to say the same.
Never heard of them, and reading their stance on a right that is Constitutionally guaranteed to “not be infringed upon”, I don’t want to know anything about them. If they automatically want to disregard more than a third of their potential customer base, I don’t see them being in business for too terribly long anyway. Someone also needs to clue them into the fact that very, very, very few US citizens own “military grade firearms”.
And this ‘stands up to gun violence’ how? More show boating for the headlines. What a joke.
So if you own one custom-engraved O/U shotgun that costs 3000-5000, you only get 2500 covered?
Wow.
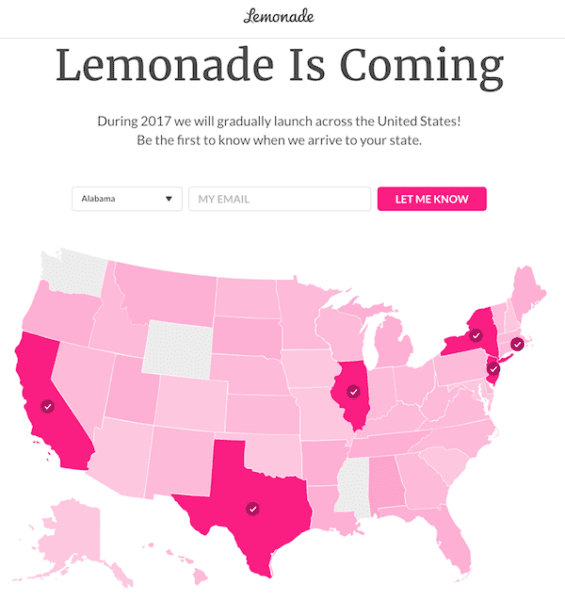
I had to chuckle when I saw that map. They don’t do business in Wyoming… amazing. Wonder why? LOL
I don’t need insurance for my guns. My guns ARE the insurance.
Why not Wyoming?
Wyoming state statute
Title 26 Insurance code
Section 26-3-7 (vii)
Insurance providers who are sex of male must have testicles.
Insurance providers who are sex of female must bathe daily.
Insurance providers of sex other than male or female are prohibited.
Their marketing strategy: Let’s capture the market for SJW dimwits that don’t own anything of value anyway.
So first.. they are counter first amendment free speech too.
So second.. they won’t cover small caliber semi-auto “assault” rifles, but will cover large caliber battle rifles, If wearing a burka.
Lemonade Insurance? Never heard of her
Look at the states they’re currently writing policies for. Well, assuming they’ve written any. Texas seems to be the oddball in that mix.
All prudent gun owners should drop this insurance, immediately, as this company has just advised those with their policies that they’ll do everything in their power not to honor their obligations after receiving payments.
Do they offer homeowner’s insurance? Because why would you need to own a single family home when the Revolution can let you stay in one of its perfectly serviceable Worker’s Apartments, Comrade?
So they are excluding assault rifles? Does anyone actually own a select-fire, intermediate caliber, military rifle that is worth less than $2500? If you have an STG 44 that you are willing to sell to me for $2500 I’d like to talk to you.
Lemonade stand
Hmm front page is “renters and homeowners insurance for urban dwellers”
With a graphic implying they pay for items dmaged by flooding.
also claiming they’ll pay out for stolen $15 headphones with no rate increase or argument on a $5 a month policy.
I’m pretty sure this isn’t functional insurance no matter what you own.
As usual with the “tolerant” progressives, they are blaming, shaming, banning, and intolerant of any views beyond their own. For a bunch who claim to not believe in morals or absolutes….
In the pro-gun ownership world, you are free to own or not own guns, zero, one, five hundred, any type, you are welcome. In the anti world, you must conform, all guns are icky, especially the extra icky ones.
Increasingly we are going to have to choose what coffee we drink, what restaurant, what bank, what insurance, cellphone, car, ice cream, websites, video streams, etc based on their world view foremost. Now go get a cup of freedom coffee and drive your freedom car!
One can understand the seeming contradictions in the antis/left/SJW/’progressive’ platform once it is understood that what they mean by “freedom” is; The freedom to DO AS THEY SAY!
I recommend that we all have Lemonade give us multiple quotes for different levels and types of insurance them after stringing them along and taking up their time, let them know that you are sorry but due to their policies on firearms your will take you business elsewhere.
California, New York, and Illinois I understand. But Texas indicated on their map? One of these things is not like the other.
Well, given their target demographic, I’d say that as far as they are concerned Texas=Downtown Austin
You just might be surprised how many California residents own firearms.
Not really 65% of Aussies refused to register their firearms when their Politicians swore on their childrens souls it would never be used to confiscate them.
. . Why should Cali be different.
When life gives you lemonade, you give the lemonade makers (and their mom) NO QUARTER.
So they’ll “broach” various issues “periodically”?
If I were a customer (which I doubt I would be), does this mean I need to constantly worry about some aspect of my insurance running afoul of their notion of some sort of half-baked “social justice” screed?
Would that mean that suddenly my 4 wheeler (if I had one) would be deemed “bad for society” and then carved out of my renewal?
And after that, my power tools?
And after that, something else?
Sure, run your company any way you like but this just sounds asinine. Insurance is mostly an actuarial activity but if you want to turn it into some bleating progressive harping, fine.
Do whatever you want to do but just don’t expect me to care or participate…
“…does this mean I need to constantly worry about some aspect of my insurance running afoul of their notion of some sort of half-baked “social justice” screed?”
Yep.
Expect, for example, if you own a big-ass HDTV that *isn’t* ‘Energy Star’ compliant for them not to cover its loss…
They are entitled to insure who ever and whatever they wish. But to pick and choose as they seem to be doing. They can take their policies and shove them where the sun don’t shine. Any gun owner doing business with them is no-one I want to know.
Nobody NEEDS jewelry or watches or fur coats or artwork, either…so hope they limit payouts on those as well.
Gun owners need to drop this company like it is on fire…
there are plenty of other companies out there.
“…so hope they limit payouts on those as well.”
They do. They are taking an even stronger stand against watercraft ($1500 limit), jewelry ($1500) and especially coins, currency, etc. ($200). So righteous. As someone else said, this is virtue signaling, nothing more.
In another life I sold homeowner’s insurance. THIS is the dumbest shite I’ve heard today(day AIN’T over). Hey how about us POTG publicize their overt anti 2A BS?!?😆😆😆😆
Wonder if NY lawmakers are going to take-off-after the Lemonade aholes like they did the NRA ? ? ?
https://www.yahoo.com/news/ny-regulators-investigating-nra-insurance-183522402.html
if not, there’s a disparate enforcement claim likely coming.
Well personally I’d advise everyone to contact their state level agencies that handle insurance certification. You might be able to actually take a swing at Lemonade and get them censured for this.
Read your Home Owner’s policy. My standard State Farm policy will only cover $2500 in firearms losses, unless you add a rider for more coverage. Just like it will only cover a token amount of US currency.
I do seem to remember limits on jewelry and furs. But since I don’t own either of those I didn’t read those sections very carefully.
So they increased payouts when you’re robbed blind by home invaders with guns? Because, you know, moral high ground ‘n crap, right?
Someone should flood Lemonade, Inc.’s email with pictures of the Lemon Party (DO NOT GOOGLE IT–YOU HAVE BEEN WARNED).
Aside from the fact that they a) Don’t know what an assault rifle is, and b) Don’t understand why we have the Second Amendment,
Astute insurance buyers should witness their policy of refusing to insure the lawfully acquired, lawfully owned property of law abiding citizens, and wait until the next boot falls on whatever they may own that might not square with this company’s moral code. Then run away from them, as fast as possible.
They started up in September 2016. Odds seem good they won’t last. They are very heavy in social givebacks. Not a company I’d go to.
https://en.m.wikipedia.org/wiki/Lemonade_(insurance)
I’m surprised they offer that coverage at all. Most insurers I’ve dealt with only cover firearms by rider but will cover the “contents of your safe up to X” which is usually around $2500-$3000.
After that it’s a rider. Either one per gun or a single one for the estimated value of the collection depending on what route you want to go/the company offers. Really, it’s a PITA because every time you buy or sell something you have to call the company and change the rider which changes the price of your policy.
Hey….. Is that an over/under Kalashnikov?
I don’t have one of those. Gotta get one!
That was my first thought. Or a dual magazine AK. A banana and a tube magazine in the same gun.
Is that even a REAL Insurance Company? It sounds even more FAKE than my ex wife’s orgasm.
dupe
Insurance companies for social good? Give me a break. Insurance is one of the highest forms of predation as a whole and has lead to a lot of crappy things in society like medical care being unaffordable by the masses due to skyrocketing costs at their behest.
This company markets insurance to “urban” people so them virtue signaling when in reality they want to be cheap is not to be unexpected. Look at their map, its largely states with large urban populations.
They’re welcome to have their product. I am in Illinois, and quite frankly I don’t want it. I also wonder if there’s any sort of “equal opportunity” laws that could be considered breeched by this. Insurance industries tend to be fairly heavily regulated. That said I doubt it would be enforced.
Not a customer and not planning to be but I contacted them to ask which definition of assault rifle they plan to use, the political one or the real one. Not expecting to hear back from them.
I’m with a few of the other posters on here; why shouldn’t we turn their own SJW BS back on them? If a baker can be forced by law to bake a cake for a same-sex wedding, why can’t these people be forced to insure any and every type of firearm?
Because gun owners aren’t a “protected class” any more than carpenters, Accord drivers, or saxophone players are.
“Lemonade Insurance?” This must be a joke. Why in the name of all that is holy would someone name their company Lemonade Insurance and expect to be taken seriously?
https://youtu.be/yhQql-ZbZmg
youse Yanks really strike me as gullible dead-shits believing this Vegas BS!
obviously, the Deep State fuckers wanna dis-arm youse…..for what?
tyranny? alien invasion?
nothing good!
if they make the slightest move to dis-arm, youse better start a CIVIL fucking WAR ASAP….just start blowing away any cunt who wants to take yr guns…
One concern I might have would be that eventually insurance companies will simply deny or cancel any coverage to gun owners if they decide the risk is unacceptable.
Mark D.
With the known statistics that nearly all firearm owners are responsible citizens where is “Ice Tea” insurance co. offering it’s range of product in direct competition? I would think it a slam dunk.
First rule of business: In order to survive the test of time is to avoid taking sides in politics and religion. The pendulum swings constantly, and eventually, this will destroy them.
But, I agree that a company has the right to make bad decisions, so I will not get in their way. It is too bad, however, that the decision makers will simply take their golden parachute and jump leaving the stockholders (i.e. retirement funds, 401K, etc.) holding the empty bag.
Lemonade Insurance? Never heard of them … USAA has no problem insuring firearms and they are big enough and have the finances to back up losses. Not sure about Lemonade but they sound small and under capitalized.
These bushiness amaze me.
You would think that they would know better than alienating a large group of potential customers.
I guess it comes from living inside a bubble where you think that everyone thinks the same.
I get who their target market is.
A quick look at what has happened to the NFL should give any business a reason to not promote a public policy that is going to piss off a large portion of the population.
Sure Google and Facebook can get away with it due to the monopoly they have.
A new insurance co?
I doubt the rest of their business plan is any better.
Another spin on the Vegas shooting… great advertising opportunities. At least they are obvious about it, although I still think it is really scummy of them to flagrantly take advantage of a tragedy to increase their revenue stream. But, hey, that’s just what we do in American business, right?
Never heard of them. Thanks to this article I don’t have to worry about never hearing of them.
Stupid name for an insurance company anyway. I don’t think I would have bought insurance from them if I HAD heard of them – their name makes them sound like children. “Hey mister wanna buy some leminayde?” “No, kid, now go away you’re bothering me. And say off my lawn!”
This Lemonade smells more like piss to me.
They are welcome to go out of business so that all their investors lose money. Yes, it’s a stupid name.
Actually know these guys pretty well. Ton of Silicon Valley & Alley money. Having trouble with customer acquisition–there is nothing special about the products. So they are trying “virtue signaling” as a marketing gimmick–that some rental dwelling, 20-something Manhattanite will buy them because they promise never to insure Billy Bob and his AR. Problem is, they have a fuck-ton of VC money in there and not really getting traction the market. Lot of cool gimmicky marketing, but ultimately if you can’t get customers in the door you don’t have a business.
$ 2500 limit on guns? My NRA membership includes that coverage free.
i love it when companies do this. Now i know EXACTLY who NOT to buy from. THANKS!
Comments are closed.