Gun control rally attracts few Women's March Armed bodyguards

Organizers claim 2.6 million women attended the Women’s Marches earlier this year. Barely hundreds bothered to show up for this weekend’s much hyped Women’s March from NRA headquarters to the Department of Justice.

The Capitol’s sweltering mid-summer heat and humidity may have discouraged participation, and added to the hot air spewed by the organizers at the microphone on Friday. Compare that crowd to this pro-gun group in Hartford, Connecticut in 2014.

Today, some time around mid-afternoon, the dwindling numbers of anti-NRA marchers will arrive at the Department of Justice. Needless to say, the sycophant media covered the sparsely attended rally that few people outside of the radical gun-hating left even heard about. And will do so again today.

The rally’s organizers claimed that “real men don’t need guns”. At the same time, displaying weapons-grade hypocrisy, rally organizers hired armed security to stand guard during the 17-mile march.

Meanwhile, the NRA, with these harpies on their doorstep, worked with Dana Loesch to produce another timely and powerful video.

Loesch does a great job calling out the women who organized the rally, Tamika Mallory, Linda Sarsour and Carmen Perez. She also shines a light on the men behind them – including “The Charlie to their anarchist angels…Daddy Farrakhan”.

From NRATV:

Like the KKK, Farrakhan is an anti-Semite who incites hatred against Jewish people by spreading conspiracies. Like ISIS, he has preached that homosexuality is a crime that should be punished by death. Like a racist, he’s incited division with statements like, “The white man is our mortal enemy.” Like a xenophobe, he sows religious fears with propaganda claims like, “God will destroy America by the hands of the Muslims.”

Tamika, Linda, Carmen: How dare you accuse me of racism and sexism and homophobia and whatever other ism or obia you’ve invented to push your radical agenda. Or should I say Daddy Farrakhan’s radical agenda.

You don’t get to call me all those things when a man you look up to and call honorable and hold hands with and take selfies with represents the exact type of bigot you pretend to march against. If you want to stop hate, start with Daddy Farrakhan. If you feel you’re “not safe,” go tell Daddy Farrakhan to tone down his divisive, racial rhetoric.

Today, the gun control dog just doesn’t hunt in Washington, D.C.  In fact, additional co-sponsors are signing onto National Reciprocity legislation. So far, nearly 218 Congressmen have signed on as co-sponsors – the number of votes needed to pass the legislation in the House.

RELATED ARTICLESMORE FROM AUTHOR

47 COMMENTS

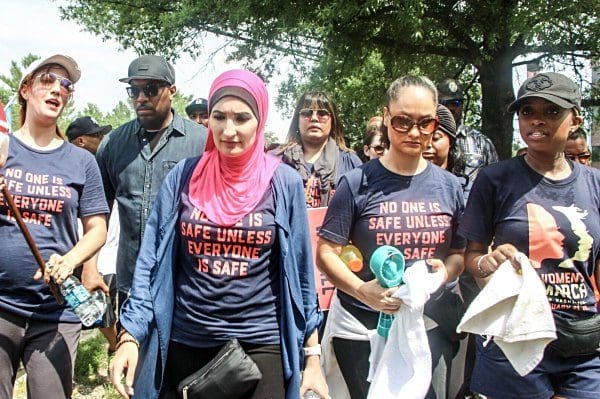
  1. “No one is safe unless everyone is safe”

    Seriously? What an incredibly vacuous statement.

    You could argue that this slogan is calling for everyone to be armed just as easily as calling for everyone to be disarmed.

    Clearly this movement is led by intellectually challenged people.

    • Especially when it is a twisting of the genuinely powerful and meaningful chant “No one is free unless everyone is free”.

      If no one is safe until everyone is safe, then we’d better get used to not being safe and prepare accordingly or just ignite the atmosphere and burn the whole deal down, because only the dead are truly safe.

      I also agree about Farrakhan, which may come as a surprise to some. I don’t agree with the snotty and divisive way she delivers the message about Farrakhan (and his ilk)’s divisiveness, nor the high horse from which she delivers it, but still…

      • Back in the 1980s, The Associated Students of MSU used my student activity fees to pay that disgusting murdering racist to give a speech about his hate. I didn’t realize at the time he was a murderer (of Elijah Mohamed, probably Malcolm X and possibly MLK Jr), but even as a teen I knew what a disgusting racist POS he was.

        The Progressive twits in student government either didn’t know or approved of it.

    • Agreed, vacuous. Somewhat heartening in a way though – if this slogan represents the actual depth of their thinking then they are certainly unarmed in this battle of wits. Also interesting is how they chose to ensure their safety – armed guards. It certainly helps bolster my argument that I am my own security guard.

    • “No one is safe unless everyone is safe”

      Seriously? What an incredibly vacuous statement.

      Clearly this movement is led by intellectually challenged people.

      Agreed but “Hope & Change” got Big 0 elected twice. Beware of stupid people in large groups.

  2. If no-one is safe unless everyone is safe, then no-one will ever be safe. Did they not think that through?
    At any rate, a good reason to carry. If no-one is safe, I need to take care of myself.

  3. “The rally’s organizers claimed that “real men don’t need guns”. At the same time, displaying weapons-grade hypocrisy, rally organizers hired armed security to stand guard during the 17-mile march.”

    Now that’s funny, right there. Almost as good as when PETA had there national conference here in Great Falls and had lunch catered at the Black Angus restaurant!

    Somehow I missed the 2.6 million march they are spewing about…

    {!-{P

  4. “The rally’s organizers claimed that “real men don’t need guns”. At the same time, displaying weapons-grade hypocrisy, rally organizers hired armed security to stand guard during the 17-mile march.”

    Now that’s funny, right there. Almost as good as when PETA had there national conference here in Great Falls and had lunch catered at the Black Angus restaurant!

    Somehow I missed the 2.6 million march they are spewing about…

    {!-{P

    • UGH!! That’s “PERSONNED” space launch!! Just because rockets look like pen!ses doesn’t mean they have to be filled with d!cks!!

      ( /S /S /S )

      😉

  6. Like asking housecats to march in support declawing or “pit bulls” to march in support of BSL.
    Madness that anyone would walk down the street chanting “disarm me!” and “render me helpless!”
    Of course, ala Sarsour, “shroud my face, beat me and lock me into servitude!”

  7. That is the female biological disposition. Little Johnny mustn’t go near a hot stove, nor climb a tree, nor ride a bike without robo cop armor, nor play dodgeball, nor keep score, nor learn any valuable life lessons of any kind while growing up fatherless.

    • Man, I don’t know what happened to you to give you that impression, but that is not “the female biological disposition” any more than rape is the male biological disposition.

      Some women are over-protective ninnies. Some.

      • Thank you. The helicopter mother thing is learned behavior, and not every woman falls for it.

        My two sons were raised on a small farm. Their favorite places to play were on top of the manure pile and sliding down the barn roof into the hay. They got hurt often, but nothing serious until the 6 year old invented the bow and arrow… and promptly shot his 4 year old brother in the eye. After we got back from the hospital, the older boy and I had a serious talk about the safety rules – with any weapon. He learned fast. The younger one didn’t need much instruction either.

    • If it were truly “biological”, then why couldn’t they get more than a couple hundred women (out of 160 million or so in the country) to show up? This kind of nannyism isn’t a “female” trait, and it’s not about being protective. It’s an “asshole” trait, and it’s about having power over other people, whether it’s just your own spouse, your kids, or an entire nation.

  8. “…rally organizers hired armed security to stand guard during the 17-mile march.” Your guns are NOT more important than my guns.

  9. A female jihadist wearing a shirt that says “No one is safe until everyone is safe…”

    Riiiiight. Excuse my snark and skepticism.

    One has to wonder when Soros will tire of the lack of results from funding the low-IQ cohort to peddle these tropes.

  11. Ah, Sarsour, if she’s involved you know it’s gonna fail.

    An Islamic Feminist, yeah, about as likely as an Islamic pig farmer.

    • Linda ‘I wish god would take your Vagina away’ Sarsour.

      Because nothing says ‘I’m totally not an apologist nut job’ like openly and publicizing mocking the victims of really bad childhood female genial mutilation who have dated speak out about their stories of their trial’s in leaving The Religion of Peace™

  12. Did Shannon’s Sugar Daddy and the Hysterical Mother piggyback on this? That would account for the lack of participation.

  13. One of the “worst” things you can say about Farrakhan is that he is not really a Muslim. Nation of Islam guys get taken to task by more orthodox Muslims for being their religions version of Mormons. And Islam usually does not take deviation from orthodoxy lightly. The fact that Sarsour (and others) can call herself a feminist and associate with heretics tells me she has gotten the blessing of the right people to practice Taqiyyah to this level.

  14. The whole “real men don’t need guns” is an argument I’ve seen many times before and it makes me both laugh and shudder at the same time.

    On the one hand it’s amusing due to your average person’s inability to fight. Overweight, middle aged guys wearing Affliction, TapOut and American Fighter gear usually are not retired MMA fighters but rather guys who’ve never trained or been in an altercation and wouldn’t bust a grape in a food fight without a significant dose of liquid courage.

    OTOH, this insane notion that fist fights are “safe” or “safer” needs to go out the damn window. This isn’t a boxing match or a sanctioned MMA fight and fighting on a hard surface is really, really dangerous. In most cases it’s untrained morons going at it, not setting their jaw and going way the fuck too far.

    Look at the guy from the ISHBADGU post a few days back. That guy probably didn’t end up in a coma from those punches (though the second one probably did give him a wicked concussion) but rather from hitting his head when he went down.

    Another problem can be seen in the “rapper vs trucker” gas station fight where the trucker puts another 20 or so punches into the kid after he’s unconscious and the rapper ends up doing this weird “downward dog” type of thing. He’s not stretching post getting his ass kicked. He’s having a grand maul seizure. Homie ended up in the hospital for weeks and came out with permanent damage IIRC.

    Real men morons settle things with their fists and often one of them pays a very, very heavy price for it. I’ve thrown a leg lasso on someone for a takedown on the mat and smashed their head so hard we had to stop rolling. Do that on pavement and homeslice very likely ain’t getting back up.

    • I was watching Daredevil on Netflix. I often thought, “well, he’s dead” when Daredevil whacked someone with a club. (Daredevil is all about not killing people in the series).

      A lot of people probably think that humans can take a much greater beating than we can based on TV and movies.

      • Right? Batman, Superman, Daredevil, etc all have this “I won’t kill, no matter what” attitude but blasting Lex Luthor through 3 corrugated steel walls and landing 2 city blocks from where he got punched in the face didn’t kill him?

        Daredevil’s body count on that show has to be in the dozens, add in all of the people he’s put into comas/wheelchairs and he has absolutely no standing to judge the Punisher (my favorite comic book hero).

        • Additionally, Daredevil specifically does not care if he puts someone in a coma.

          If I had super powers, I would totally kill bad guys the system cannot handle. If I could stop them and didn’t, I would be responsible for whatever they did because “with great power, comes great responsibility.”

          I’d also rob the crap out of drug dealers because I don’t need to worry about bills while I’m saving the city.

  15. “No one is safe unless everyone is safe” sheep being led to their future slaughter by a feminist radical Muslim who’s called for Jihad against the President of the United States.

  16. I personally think these people are the best thing Pro 2A people have going for our cause. The more these nut jobs march and chant the more real Americans look the other way. Much like the boy who cried wolf. The same lies told over and over get tiring to people you have more important things to worry about in their lives. Like jobs,taxes,health care and crime. Most hard working Americans have no respect for these people because their clamoring becomes white noise against the real life problems they face. So let them march and chant.

  17. If you want to be safe don’t get involved with drugs and gangs, don’t live in crack central then you will be safe. Pretty simple for people not brainwashed.

  18. Linda Sarsour is a dangerous person, all she wants is power, she actually scares me.

    • Loathsome Linda craves power, so let’s hope she becomes chair of the Democratic National Committee. That will lead Dems in the direction we want. Off the deep end.

      Sarsour will then open the 2020 Democrat Convention with an earsplitting “ALLAHU AKBAR!!!!”

  21. “real men don’t need guns”

    I seriously doubt that any of those sows is an expert on “real men” and what they need.

  22. Dana said…”biiiiiitttttcchhhhhhh”.

    That vid didn’t seem super scripted like the some others Ive seen. She seemed legitimately pissed off.

  27. These are dangerous wealthy women who don’t want poor women, or anyone else, with the ability to use lethal force in self-defense.
    Having a “rainbow” of people to sell their message means nothing.

Comments are closed.