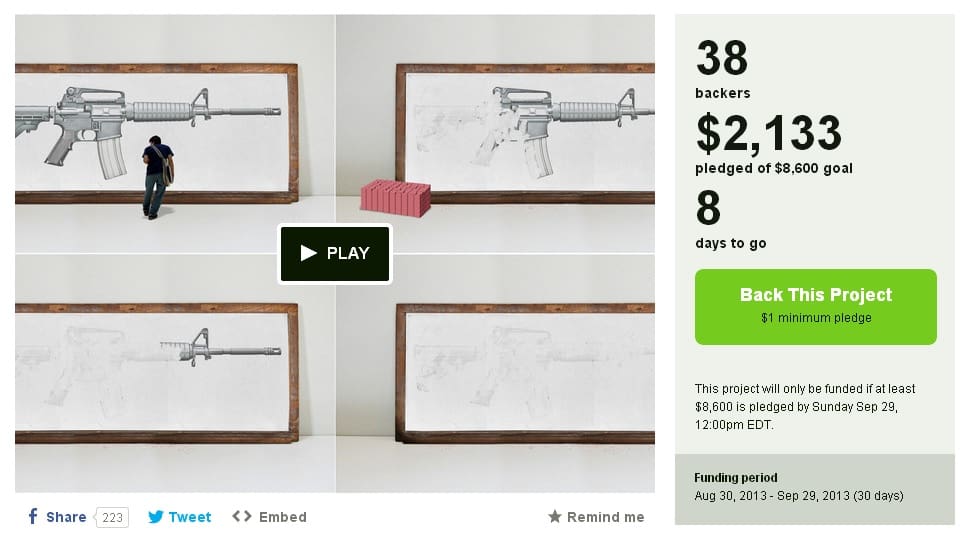
Greg Bokor, a Massachusetts artist, is looking for Kickstarter funding for his entry into an upcoming art exhibition. It’s a 20 foot long Bushmaster AR-15 drawn in pencil, which he invites people to pick up a provided eraser and well, erase part of. He’s time-lapse filming the whole thing. He wants it to be a symbol of… something. He really hopes “to get some victims relatives to be the first to erase” and to do that, he may need your help providing airfare. Give ’til it hurts, folks. [h/t: TJ]
Pedro Reyes, an artist from Mexico City, had an idea what to do with a bunch of the weapons seized by the Mexican army, which are usually buried or destroyed. After they were de-mil’d, he turned them into mechanized musical instruments and used them to make beautiful (?) music. Something about the sight of AR uppers and lowers clapping together as percussion is sorta amusing. It appears that the a lot music is not actually being played by the former implements of destruction, but that they took a representative sound and then sampled it up and down the scale to make the notes they needed. But hey, this is art, right? It doesn’t have to actually mean anything. [h/t: Corey K.]
In case you missed it, the University of Kansas professor who sent a Tweet wishing death on NRA members children (maybe), has been placed on “indefinite administrative leave pending a review of the entire situation.” Actions have consequences. Even a liberal arts professor can see that, surely.
Emergency Management magazine has an interesting opinion piece about Why Emergency Managers Shouldn’t Alienate Preppers, and how not doing so can make Managers much more effective in their mission. “It’s important for emergency managers to understand that preppers are a cut-above the vast majority of citizens when it comes to emergency and disaster preparedness.” [h/t: Chip K.]
An American national traveling on business in India is being held after he was found in possession of (gasp) live bullets. After getting off a plane at Biju Patnaik Airport in Bhubaneswar, William Hurtubise was going through security prior to boarding a chartered helicopter when “at least eight .22 caliber bullets” were found in his medical kit. Mr. Hurtubise professed ignorance of their existence, as they had apparently been traveling around with him unnoticed for the last six months, including when he boarded the flight in New Delhi from which he’d just deplaned. He is being charged with “illegal possession of ammunition without any licence,” and potential punishments are unknown at this time. The US Embassy is involved.
Urge California Governor Jerry Brown to VETO gun control bills here: https://www.firearmspolicy.org/the-issues/california/2013-2014/askbrown/
Any artists on TTAG? Lets roadtrip to MA .Bring your sharp pencils and photos of your favorite AR accessories.
It’s a dirty job,but somones gotta do it.
That would be awesome. After all, he did invite the public to contribute, and the meaning of all art ultimately depends on its viewers…
How about bringing sharpies and redrawing the AR so it can’t be erased.
Sharpie – the modern day Constitution ink – formulated specifically for enumerating rights of men and limits on Government.
I’m not too much of an artist, but I’m game.
Think of it as a tracing back in freedom 😀
lightweight. let’s road trip to India.
Best thing to add would be a drum mag. Those have a funny way of making liberals’ heads explode.
I live in MA and would gladly help…..except this is being entered into an art display in Grand Rapids, MI. Details are in the kick starter page.
I say let the grabbers spend their time and money on pointless displays like this. Let them feel like they are “doing something”, while they are in fact doing nothing.
If I gave money to this bilge, it would hurt.
Is it just me or is it odd the TTAG is givin these nutjobs airtime???
RF’s is a business man. A little waving of the red flag under our noses gins up the number of hits on the site so he can charge for adverts. i have no problem with this as it keeps TTAG going.
That may be true i never thought of it that way.
RF had nothing to do with this. The Digest is my baby, excepting his publisher’s prerogative to edit it, which hasn’t really happened yet. I put the stories in because I think they’re amusing, or interesting, or intriguing.
I stand corrected. Still, if it fills RF’s rice bowl, it’s good for us that like TTAG.
You want erasing art? How about a drawing of congress and everyone who has lost someone due to the things they pass can go erase a line. That picture will be gone in about 10 seconds.
Id just light it on fire and save everyone the time 😉
Preppers are prepared? WOW. What a revelation. That guy should hook up with Siegel for a future study.
Bokor wil follow this up with a giant pencil replica of the Constitution.
Very well played. Also, f!ck that guy.
I wish I’d thought of that. Then something like, “Obama will be first in line for an eraser.”
I would contribute to his Kickstarter fund, but I’m not sure what the exchange rate is on a pair of my extended middle fingers.
Two individual 1 cent contributions.
I like the Sharpie idea. About 30 people could make it happen before they had time to notice what was going on.
Seriously, i have nothing going on. Let’s get some people together and plan a route.Is anyone a man with a van?
I got a 70’s model Dodge Ramcharger it’ll haul more than a new Econoline lets load up and go
Does a donation come with a chance to kick him in his hippie BA11s
Artist think their special and so much smarter than everybody else.
Screw them (head in the clouds liberal shits)!
Smitty
Some people have an irrational, unhealthy fear of the AR. I feel sorry for them, nah, not really. I think they are myopic and lack critical thinking skills. I am sure they would sign away their rights for all of the imaginary safety in the world.
It would do members of emergency managment teams across the country very well to not look at ANY gun owners poorly. They might just be surprised how many people in Fire/EMS are gun owners.
Why didn’t he draw a picture of SSRI’s (Selective Seratonin Reuptake Inhibitors) or perhaps a picture of a gun free zone sign? Since he’s in MA maybe just a collage picture of all the legistors that have championed gun free zones, starting with my favorite Congressman John Tierney, who’s wife is a felon and posted for new gun control less than 4 hours after the DC shootings, when they were still saying an AR was involved. Yes erasing him (through legal means via the electoral process of course) from the political landscape would make this county significantly safer and more free.
Any artists around here want to do a reply artpiece of the Constitution and invite this “artist” to be the first to start erasing it?
Sad thing is, he probably would.
I wonder if the irony is lost on him that free men with military rifles are the reason his pissant state exists.
The Wisdom to Know the Right;
The Will to Choose it; and
The Strength to Make it Endure.
http://en.wikipedia.org/wiki/File:Minute_Man.JPG
They should do this. Then, when it’s totally erased, rip off the top sheet to show another drawing showing an confused, empty-handed cop, drawn in pencil, facing a masked man with a handgun, drawn in ink. Now that’s art: think about whom you’re really trying to disarm.
From the artists’ bio: “I believe art, created by people who tend to think differently, can encourage the viewer, who may not naturally think differently, to do so.” He is a superior being, apparently, and is doing society a favor by explaining things in a way that even idiot gun-nuts like ourselves can understand. Wow, elitist much? Jerk.
He has a point. I used to think art was the ultimate expression of humanity and a wonderful reflection of our special place in the world. Then I saw someone put a crucifix in pee and call it “art,” and I went from respecting art as an institution to wanting to stomp a mudhole in every annoying fruitcake who wastes NEA grant money –That I had to pay for!– on stupid bullshit.
Massachusetts. That says it all. I left there for AZ in 1995, and I’m enjoying here in America.
Not all artists are playing jokes on the public. Some are just genuinely mad.
I don’t believe I’m mad, but I’m certainly pissed off.
Pedro Reyes, an artist from Mexico City, had an idea what to do with a bunch of the weapons seized by the Mexican army, which are usually buried or destroyed.
Yea right. The Mexican army (on cartel payroll) likely hands to to the… you guessed it… Cartel.
BTW, India is one of the most corrupt places on planet earth. They don’t want any dissident citizens and they certainly don’t want them to have any ammunition!
Hey guys-
This “art” has been entered in the 2013 Grand Rapids Art Prize competition. There is also a pro-gun entry in the competition entitled “Model M1911” you can view it and see how to vote here- http://www.artprize.org/andrew-keson/2013/model-m1911 Anyone can vote and I hope that even you Glock aficionados will help make sure the pro 2A piece gets more votes than this garbage. Even if you vote for a 1911 inspired piece you can still keep your 1911 haters club card, I promise (I checked with James Yeager, he said it was cool).
Someone should draw a picture of Feinstein’s last AWB Bill and put it down range, and have .22s available so each viewer can shoot a small hole in it until it disintegrates.
-D
“He is being charged with “illegal possession of ammunition without any licence,” and potential punishments are unknown at this time. The US Embassy is involved.”
The US Embassy is involved? Given the proclivities of our current administration, does that mean that they’re helping to sharpen the sabre to be used in the beheading?
That American in India should be sentenced to time served; being in India is punishment enough.
Comments are closed.