The anti-gun agitprop propagators at thetrace.org have got their proverbial knickers in a twist over the fact that some states “allow” citizens to carry a concealed weapon without applicants proving (to the state) that they can “hit the broad side of a barn.” Most TTAG readers agree that state-run concealed carry licensing — regardless of its requirements — is an infringement on Americans’ natural, civil and constitutionally protected right to keep and bear arms. Given that constitutional or permitless carry is a pipe dream for many states (e.g. New Jersey), should their courses have a mandatory live-fire component?




Wonder if they would support a test that required you to pay to take it, prior to being allowed to vote.
No probably not… Because racism(sarcastifont implied)
Now wait just a minute… do they want us shooting our guns or not? I’m getting mixed signals.
Well when you’re trying to put forth manipulative emotionally driven material to scare people, being inconsistent and sending mixed messages is irrelevant to the end goal. For example, to use guns you need super Hollywood movie special forces like training to even hit your target, while on the other hand, it’s so easy that any disaffected youth can become the next Lanza or Roof and rack up huge body counts.
Propaganda narrative driven journalism at its best.
Me thinks they want us to fire at live targets. I mean, that’s the only real training right? The kind that shoots back.
No,
I shouldn’t have to be skilled at protecting myself.
Any effort made to defend ones self should be acceptable.
I may even want to carry it empty in hopes to scare away an attacker, my choice.
Before comparing drivers licenses, that’s a privilege, not a right.
As US citizens we have the right to keep and bare (own and carry) guns from birth. We should not have to jump through political hoops to exercise this right.
I do love for people to seek training on their own. But it should never be a requirement. Should there be free speech training?
One of Robert Heinlein’s favorite characters, the matriarch Hazel Stone, hero of the rebellion to free the moon from Earth’s domination (The Moon is a Harsh Mistress/The Rolling Stones/The Cat Who Walked Through Walls, and others) ALWAYS open carried her blaster. And frequently kept its magazine filled with breath mints.
“Scaring away” an attacker with an unloaded gun is brandishing. If you’re going to use a gun, make sure it’s a situation where you actually need to kill the attacker to stop him from killing you, and shoot to kill. Shooting to “stop” (shooting to someone in the arm or leg, or a “warning shot”) will result in you being stripped of your rights, losing your job, house, and family, and being thrown in the slammer while Jamal gets to rob, rape, and kill other families.
You should never shoot to kill. In defense situation you can shoot only to stop imminent attack on your (or other innocent person’s) life and limb. Best way to stop such attack is hitting center mass of attacker until he stops being dangerous. If in the process he dies – well too bad, but it is never your goal.
Of course I would strongly suggest anyone who wants to get a carry permit train with their weapon. But I’d never want it required, for the simple reason that all the State has to do at that point is make the training requirement too difficult for anyone to be reasonably successful. “OK, if you want your CCP we want to see a 5-shot group with no deviation more than 1 minute of angle at 100 yards with your pistol. If you fail you have to start the permit process all over from scratch, and your fees are non-refundable by the way.”
They actually tried requiring applicants in DC to perform their shooting qualification in the city. There were no ranges in DC at the time. I don’t think that one was passed but it gets to the heart of their intention.
Not to mention that when combined with other proposals like $100 tax/round, limit 10 rounds/year and a 50 round minimum to qualify ties that up in a nice, tidy bundle.
O2
When you are teaching concealed carry basic personal protection, you hopefully are teaching proper use of the pistol. If you are at 100 yards you have time to retreat from danger if you are intelligent. Personal protection begins when someone is close to you and acting in a violent manner.
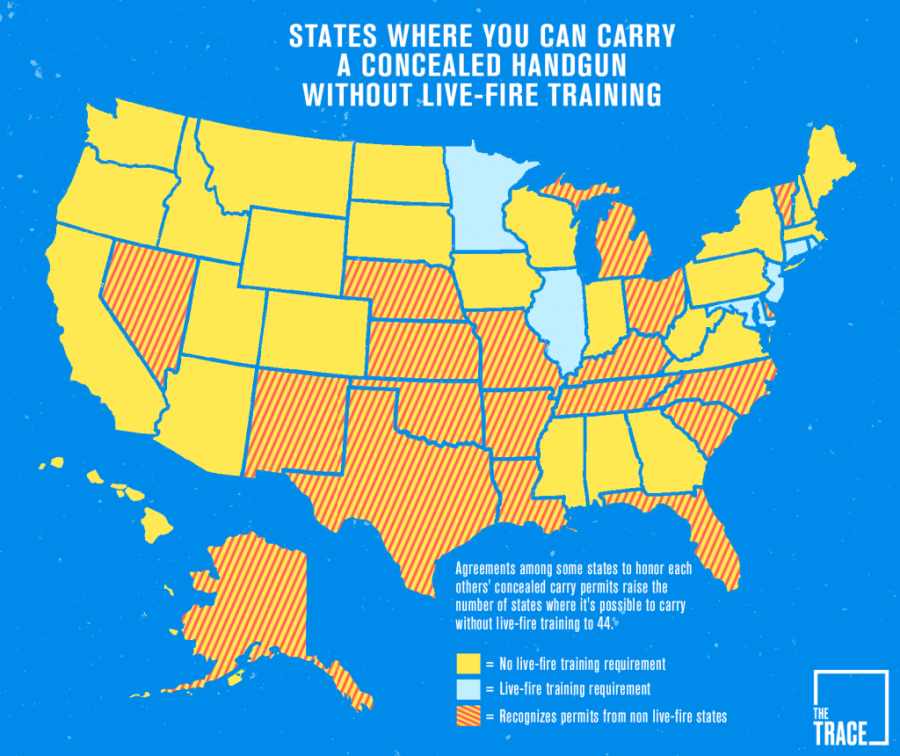
Is the source information correct? Requirements could have changed (improved) since then, but both in 2011 in Missouri, and in 2013 in Ohio, when I obtained carry permits for each state, a live-fire component was included and required.
Not so in Indiana, though – and shockingly enough, there’s no blood running in the streets.
No blood running in the streets in Iowa either and I qualified with a free 20 minute online course from the Maryland Police Association (thanks Des Moines Register for the hat tip on that one). Iowa is consistently in the lowest 5 states in homicide rate.
I didn’t get a “Harumph” outa that guy
Click through and look at the other chart accompanying their article if you dare, Chip. Missouri and Ohio are shown as requiring live-fire, so is Florida, mistakenly, although many trainers in FL will try to tell you that it is required to pad their fee.
We did lower our class time from 12 hours to 8 hours in Ohio, though, which still includes 2 hours of rangetime.
Florida requires live fire training:
790.06 License to carry concealed weapon or firearm:
“A photocopy of a certificate of completion of any of the courses or classes; or an affidavit from the instructor, school, club, organization, or group that conducted or taught said course or class attesting to the completion of the course or class by the applicant; or a copy of any document which shows completion of the course or class or evidences participation in firearms competition shall constitute evidence of qualification under this paragraph; any person who conducts a course pursuant to subparagraph 2., subparagraph 3., or subparagraph 7., or who, as an instructor, attests to the completion of such courses, must maintain records certifying that he or she observed the student safely handle and discharge the firearm”
http://www.leg.state.fl.us/statutes/index.cfm?App_mode=Display_Statute&URL=0700-0799/0790/Sections/0790.06.html
As with everything Bloomberg’s minions do, the information is twisted to fit their narrative. For example, North Carolina requires a live fire component as part of the CCW training class. It has been a while, but I think it was a total of 30 shots at 5, 10, and 15 yards and I think 21 of those need to be in the black on a silhouette target.
In reality, they should have shaded NC blue with red stripes as NC will recognize CCW permits issued by all states (as it should be everywhere) but still requires live fire for their residents. So they are trying to paint it as all of us are untrained yahoos that didn’t have to put a shot on paper because NC welcome’s all CCW carriers. The reality is that by law, NC residents must be at least 70% proficient…
I assume that’s because it all froze into ruby red sheets of ice? Blood can’t run in that sort of climate : ))
Source is a mish-mash: e.g. Arkansas requires a range training component for a Concealed Handgun License. Yet the diagram only indicates that the state recognizes other states that have no requirement. Likewise Texas requires a range component.
This (the diagram) is the kind of fuzzy headed thinking that gets a poor grade in sophomore writing classes.
I believe in Ohio you can open carry without a license as long as you are legally able to own a firearm.
The RTKABA doesn’t come with a requirement that you can hold one. A quadriplegic has no less RTKABA even if they have to crawl over to their weapon and fire it using only their lips.
There are few more perishable skills, there are far too many experts trying to sell you a “mandatory” course.
AND FAR TOO MANY OF YOUR FING NEIGHBORS THAT WANT TO BE THE GATE AND PORTAL TO YOUR RTKABA.
F’ em
Absolutely not.
That being said, some type of training would be in the best interest of anyone choosing to own a gat. But required? No.
I’m with Tom: no state mandated training. Besides, Gunsite and other private courses and competition are typically much better than government training. The “evil” NRA has a lot off excellent safety training and programs.
In CT, the mandatory course for getting a handgun permit (to buy, own and carry a handgun – no permit, no handgun at all) is the NRA basic pistol course, taught by an NRA instructor at a local private range. Overall not that onerous (it’s an 8 hour course, we were done in well under 6), and the course was very well run and presented. Plus of course it introduces new shooters to the NRA in the form of a really friendly former high school teacher who now teaches guns. Since the range where I took the course was located in the very “diverse” town of Bridgeport, the NRA might have even recruited the next Mr. Colion Noir – who knows?
But at the end of the day, an Enumerated Right should not have a training requirement. In this imperfect, fallen world, the NRA pistol course isn’t a bad way to go.
From what i understand most if not all counties in California require range qualification for a CCW.
Training? Yes. Training in almost all instances is a good thing.
Mandatory? Absolutely not! Slippery-slope argument of training this year is 2 hours, next is 4 hours, and in a few years becomes days, becomes weeks, where does it end?
AZ no longer requires a permit to conceal carry, so, that’s a bit inaccurate.
I support live-fire training but I don’t trust the State to enforce/develop the curriculum for it.
The only training that should be required for an unconstitutional weapons carry permit is free class provided by the state to teach applicants how to avoid running afoul of all the other unconstitutional firearms laws in the state. Further, all permit holders should be informed of any changes in laws pertaining to weapons and self defense. Proficiency with a weapon is none of the states business.
yep and they should throw in a substantial tax credit incentive too. If it saves one life.
There is a bill that has been proposed this year in Indiana to offer a tax incentive for training.
As the old joke ends: “Now we’re just haggling over the price.”
O2
Heh. Always a favorite…
So California and NY don’t require “live fire” for a permit? I thought they both required a fairly expensive class with a state-approved curriculum?
In those jurisdiction where it’s conceivable to get a CCW, the cost has been estimated around $600
Thanks DrV. I think their map is kind of like their “100’s of school shootings since Sandy Hook” claim.
California has a requirement of “up to 16 hours of training,” part of which is classroom in which safe gun handling (introduction to handguns, essentially) and part is the law on concealed carry and use of force. The other part of the training is live fire, with various instructors having students shoot various number of rounds, usually 100-200. The requirements vary by county as to whether a shooting qualification test is required (that must be passed for a license to be issued, after all other requirements are fulfilled). One county, so I have heard, requires an applicant to pass the same qualification test as a LEO applicant, at ranges from 3 to 15 yards. Costs obviously vary by location. Around here in far northern California, the class runs roughly $150 (renewal classes are $40 or $50, and have only a four hour classroom component). The application is about $160, but some counties will require a psych eval. (statutorily capped at $100 as I recall, and the same eval. as required of LEO candidates).
I do not know of any county that does not require live fire training for the initial application. None, so far as I know, require it for renewal (but it would not surprise me for the “barely issue” countiues).
Ny requires a class but not live fire. This is because it is illegal to handle a pistol without a permit. Want to handle a pistol at cabelas? Need a permit. Want to let your buddy try your pistol at the range? He better have a permit. Getting your permit and want to hold some guns to see what you might like to buy? Drive to a range in Pennsylvania.
South Dakota recently began issuing an “enhanced” permit with the intent of expanding reciprocity with other states. Unlike the basic permit that costs $10 and relies on only a NICS check, the enhanced requires 98 rounds be fired. Why 98? No one knows, but it was fun to shoot and show off.
I also was required to shoot for the Minnesota and Nevada permits. And to actually drive a car for my first drivers’ license.
Should states have this kind of power? Strictly, no. Better the states than the Fed though. And I am more comfortable knowing that all the drivers on the roads had to demonstrate their ability to drive before being given a license.
“And I am more comfortable knowing that all the drivers on the roads had to demonstrate their ability to drive before being given a license.”
And you know “all the drivers on the roads had to demonstrate their ability to drive” how? Because their car won’t start unless they insert their currently valid license in a slot on the dashboard, and press their thumb against a bio-reader to verify identity? Because NO ONE would EVER consider doing anything in violation of a law (like drive without a license, or insurance, or driving while impaired)?
Puh-leeze.
The biggest difference I see between these two areas, is a vehicle MUST be used (driven) to gain anything of value from it, whereas a defensive firearm MAY successfully ward-off an attack just by being present in the owner’s hands. Is that the way to bet? No. Do I primarily subscribe to that method of use alone? No. Is it a true and accurate depiction of firearm vs vehicle use? Yes, it is.
Point taken on unlicensed, uninsured or drunk drivers. I’m not one of those, and presumably you’re not either. Surely you’re not suggesting that we should be like them?
No, just suggesting that the training and licensing you are endorsing does not do what you claim it is doing.
Same as with guns.
All those driver’s licenses, and how many car crashes, and fatalities and injuries resulting from those crashes, every year? By comparison, how many accidental injuries and fatalities are caused annually through negligent discharges and other unintentional misuse of firearms?
Training can (theoretically) reduce adverse events caused by accidental use of something. It cannot reduce adverse events caused by intentional use of something.
Firearms owners are already ridiculously safe in their use of firearms. Mandatory training and licensing do nothing to improve that safety.
A great point, well made (as usual).
Chip is exactly correct. There is about 500 deaths due to firearms accidents each year. This is approximately the same as deaths due to lightning strikes. It would be equally beneficial (or wasteful depending on how you look at it) if the government required lightning strike safety classes.
Statements like these are why I feel this country is doomed to continuing government over regulation. For example, AZ issues DL’s that are good until a person is 60 years old. Theoretically, a 16 year old doesn’t have to retake a DL exam until they turn 60. The AZ vehicular deaths per 100k is 12.8 while SD is at 16.0 per 100k with a standard 5 year renewal. What does it “prove?” Nothing, except state-issued DL’s are not a good indicator of safe driving.
I recently (finally) took the IL CCW classes and one of the requirements is a live fire test.
It’s a complete joke. 10 shots each from 5, 7 and 10 yards. The state requires 70% to pass. My instructor wanted us to get 100%. I’ve been practicing for a test consisting of 10 shots in a row on-paper on a Rapid Fire pistol target at 50 feet, so the IL requirements were a breeze.
Out of the 20 or 25 people in the class, only 1 had any trouble making it on the first try.
Should it be required? No.
California most definitely requires training and a test.
These morons hate it when you do fire a gun and they hate it when you don’t fire a gun.
No better than toddlers throwing tantrums because emotion.
^This!
Just like they hate when you buy ammo in bulk to train with and then they say civilians don’t train enough; followed by the assertion that if you train a lot, you live in a fantasy world and are paranoid about something that is never going to happen; followed by “you should give up your guns because (insert crime/mass shooting/terrorism) happens all the time.”
Well said.
Just like the guns are either too small (easily concealable handguns), or too large (so-called “powerful” assault weapons and .50 calibers); hold too much ammo (high-capacity mags!!!) or too little (easily concealable handguns, again); aren’t accurate enough (the old Saturday Night Specials), or are too accurate (sniper rifles!!!).
They go back and forth, using whatever they can to influence and inflame the raging emotions of their knee-jerk low-info members and voters.
Perhaps we need a cooling-off period of 5-10 years before any proposed new anti-gun legislation can be passed after a mass shooting? You know, to protect our children’s gun rights (it’s for THE CHILDREN!!!).
It becomes very simple when you realize that ANY statement, condition, or complaint made by a gun grabber means “Fuck off and die, you shitstain gun nut!”
Are they going to pay for it? The way I see it, any mandatory class should be readily available and paid for by the state.
Not an ideal situation, but let’s have the lefties put their money where their mouth is.
Give them full control of it, and it will become improbable/impossible to achieve that much more quickly.
NYPD would have problems with this.
Delaware just makes you spend hundreds of dollars, weeks of time, and shames you into public announcing you intend to carry while requiring permission from 5 other people. And the courts. At least we have open carry for now
Doesn’t the conceal carry permit apply to other weapons besides firearms in stone states? I know it does in Wisconsin. Why should someone have to qualify with a handgun in order to carry a kubaton or a knife?
Shouldn’t be required but it should be highly encouraged.
Same with accidental death insurance if you use you kill someone you didn’t intend to while carrying.
What kind of incentive could be offered for taking a gun-safety course which included live firing of their weapon? Not penalties, incentives or rewards. An offer of 1/2 the price of two boxes of ammo? Just bring in the spent shells and receipt for the rebate? Goes to first-time concealed carry licensees only perhaps. Something like that?
How about no permit fees for the next application cycle?
Do 3 courses of increasing challenge levels in 5 years, get free lifetime permits?
if the trace wants to pay for it (range time and ammo, and offer it at all hours convenient), I’ll be glad to show up and frighten them with my proficiency.
Don’t think you should be “required” to get training for a permit. But, if you go the extra mile to get “approved” training, you should get an “enhanced” permit that gives you the right to carry ANYWHERE……….school, govt building, airplane…….WITH reciprocity in all 50 states and DC. Just my two cents.
Then the state .gov should pay for the ammo since that becomes a barrier to a Constitutionally protected right.
Should some/any states require mandatory live-fire training component for open and/or concealed carry?
If no live-fire training is such a huge danger, then why are armed people shooting bystanders at the same rate (basically zero) in states that do not require live-fire training as well as states that do require live-fire training?
Thus the answer is “NO”, we should not require live-fire training.
Having said that, it is always good for our nation to promote training and responsible lifestyles. If live-fire training is so important, then Big Brother can provide live-fire training for people who cannot afford it. Big Brother could also increase the legal liability for armed citizens who have no live-fire training and injure bystanders.
I teach the NRA Pistol Class which is a requirement for CT Permit and it has a Live Fire component to complete the course.
I follow the NRA Guidelines. IMHO, the NRA Pistol Class is the minimum and nothing more. If the requirement is simply to go through the NRA Basic Pistol Training Class, I see zero issues with that. I teach the basic pistol sight picture, grip and function of pistol using a functional replica airsoft P226 prior to going to the range. Everyone I have taught thus far, has been able to shoot properly and many where first time shooters.
The current course requires you to fire 5 shots each into 4 3″ circles from 10yrs. That can be accomplished by anyone.
Prior to that requirement I had students shooting into 4″ circles and while nobody was shooting a single ragged hole, everyone was able to get inside the circle at 10 yrs.
I don’t see the problem, as I state again, as long as the requirement is not more than what is in the NRA Basic Pistol Class.
I took an NRA Pistol course to get my permit in Wyoming (before it became a Constitutional Carry state). My instructor had us do live fire training as well. Why Wyoming is considered one of the No-Fire states on the map is a mystery to me.
The nice thing about training in anything firearms-related is that it tends to be a whole lotta fun doing it. Most people I know who have a CWFL can’t get enough of going to the range.
However, due to the nature of guns and ammo, there is a dollar figure attached to it, which is the burden that mandatory training imposes. The right of armed self-defense shouldn’t be the province of the rich.
Show me the data.
Show me the state-by-state data on involuntary manslaughter, negligent homicide, whatever you want to call it, caused by the poor marksmanship of someone shooting to stop a deadly threat.
Compare the Constitutional states, the permit without live fire states, and the states requiring a live fire test.
Until then, stick it up your…
Safely defending yourself with a firearm requires the ability to think clearly and make good decisions under extreme duress. Marksmanship really doesn’t factor into it. We read stories on a weekly basis about some octogenarian with no experience or training perforating some thug. May it ever be thus.
I guess I am confused about that chart. Texas absolutely requires live fire to obtain a CHL/LTC permit. 50 rounds to be exact, and at three different distances. Texas also recognizes a few states that doesn’t recognize us. California, for example, is good to go in Texas but not the other way around.
Yes, it’s over-simplified and out-of-date in a couple of areas.
Simple is all these people know or can handle, it seems.
My class included it but it was a 22 revolver, hardly a firearm to show proficiency. My concern was in our class there were women who couldn’t rack a slide on a 9MM or figure out how to keep the cylinder of a revolver open by inserting two middle fingers around it while holding the gun. And most of these people leave with a certificate. Everyone can use more training and education…
MA has no shooting practical test and there is definitely blood in the streets. Okay, the blood is mostly from drunk drivers and the gangs in Springfield, but blood is blood. Right?
No….no….and no.
2A isn’t about skill level.
Period.
I was surprised to learn my sister-in-law has an Idaho CCW for a pistol she has *NEVER* fired.
I can’t even imagine… like having a new toy and not playing with it!
I have to Question their Data. Their data says that “live fire is not required for California. California does not recognize any other state’s CCW so “Live Fire” in another state is not strictly required but the CCW is not recognized so it is not an issue. While it is not required to actually shoot to purchase a weapon in California it is required to Shoot, Prove your safe weapon handling and marksmanship in order to qualify for a CCW.
Live fire testing and training should take place in high school and be offered for free in all community collages that receive public funding.
In Maryland we have a live fire requirement to obtain a Handgun Qualification License, which is necessary just to buy a handgun. (Forget about a carry permit; that’s nearly impossible to obtain in Maryland.) The rules for a HQL don’t specify that you have to hit a target or even shoot at a target. Just that you have to fire at least one round. I know at least one HQL instructor who has his students fire a .22 LR piston into a bullet trap. Meets the live fire requirement, but what a joke.
MN has live-fire requirements, but I’m pretty certain it’s up to the instructor on how many rounds and caliber, or if the carry piece must be used. I’ve spoken with people down south who fired one magazine full and others who’ve fired fifty rounds. Depends on season and available facilities, I imagine. I know my instructor would not stand outside in ten below weather while twenty (or however many- all the classes I’ve been to had more) students fired off their fifty rounds.
Not that I think there should be a permit testing process of any kind, but I do think all applicants should be required to demonstrate proper weapons handling and shooting skills at a bare basic level. Reason being: this is the 21st Century and not every man, woman, and child is raised with a firearm as a means of having a meal or defending against banditos (though that time seems fast approaching).
I can get behind live-fire training requirements. In fact, it’s so important that everyone should have to take it, regardless of whether they are pro or anti gun. It can be a fourth “R” for education – reading, writing, ‘rithmetic, (R)msmanship. Can we get a change.org petition up?
In CA I had to do 70 rounds per each gun to be listed on the permit (up to 3), and yes, those are the only guns you can carry. So 210 rounds total on an FBI silhouette at 3, 5 and 7 yards, and you had to score 70% hits. And I saw people who failed. There was an elderly lady who just couldn’t hit with her j-frame DAO at 7 yards. I bet she could still defend herself with it.
So long story short: no, live fire requirement is not a good idea.
And before you ask, between training, background, ammo, etc. it costs about $500 to get a CCW. Not counting the gun.
But the weather is nice.
I not only think this is a good idea, I would go much farther. I would suggest that every citizen should have to qualify with both rifle and pistol, before being registered to vote, or allowed to carry a gun, OC or CC, or to work as a journalist or newsman.
The Minnesota shooting requirements are very vague. In my classes all I look for is that you can handle and discharge the firearm safely. There was a case in Minnesota where a vision impaired man was suing for discrimination because he was denied a permit to carry. It came down to he could not safely identify anything beyond his target. So he went to another state and now a blind man has a permit carry. I think reasonable shooting requirements are necessary.
William
Pistol Safety Instructor
Range Safety Officer
I escaped from Western NY this past Summer to TN but I did have a CC permit in NY. No training required, cost around $130 for what was suppose to be a life time permit, which later they decided to make 5 years so they could charge some more and check their gun registry. Permit was required to even own a handgun and every handgun you bought had to be put on your gun card that you carried in addition to your permit. In our county it cost $14 for each gun you added and took 10-14 days to add before you could pickup the handgun that you had already paid for. Process to get a license took me a little over 6 months and I lived in a gun friendly county, most off the delay was the states part.
TN required an 8 hour course with live fire, varies in price, the one I took was $50, lots of clubs and stores offer the class. Class was similar to NRA basic pistol course. Took about 14 days total to get carry permit (TN does not care how you cary it), I could check online for status and it was approved the same day I submitted the last paper work, the delay was making the license and mailing it.
In Israel every 3 years we need to renew our permits by shooting 50 bullets from 6 and 10 meters and safety training. Takes about two hours total to complete.
I actually think it’s good think to force people that carry to have a safety and shooting training , usually the people that heart are not the one that hold the gun.
“I actually think it’s good think to force people”
Sorry. Not a fan of forcing people to do things…people that are otherwise law abiding folks simply minding their own business and living their lives.
I get the arguments for ‘constitutional carry’, but I actually think “shall issue” is about right.
Why?
Because I think it is important that people know the law of their land and some basic decision matrix training; were they can carry, when they can (and cannot) draw their firearm. What is considered self defense, assault, or brandishing. And what is not. Going over the basics firearm safety. What nearby states you can carry in as well (until we have universal reciprocity, that is).
Live fire should NOT be a requirement. But opportunities for new gun owners to either obtain further instruction on live firing and functional operation of their firearms should be made available at the end of the class.
In other words, ‘situation awareness’ of the laws and behaviors to keep people, especially the new ones with short attention spans, out of trouble.
it should be done. And then like our forefathers, there should be a keg waiting once the training is done.
Whether it should be mandatory is a thorny issue.
Their data in accurate; in NC we’re required to demonstrate proficiency (even though its at ~3, 5, and 7 yards), at least for the initial license.
I read the map legend too quickly; my bad.
+1000000 Chip(as per usual). No Indiana bloodbaths. Meanwhile in MY state of Illinois I need 16 hours of “training”, a FOID card, fingerprints,etc. And several hundred bucks… Even though I’m a really good shot and proficient. Part of the “shall not be infringed” phrase.
Do i have to pay to prove that i can speak properly before I’m allowed to use my Freedom of Speech? Am i required to pay or pass a test to use my Freedom of Religion? Am i required to pay/pass something to use my Freedom of Assembly?
Then why start here?
To the best of my recollection, l had 6hrs class time, 100rounds live fire here in Michigan. There is talk of enhanced classes enabling you to carry in restricted areas, like stadiums, bars and such. I’m sure it will come at a price, if and when it happens. Personally, l like the idea of constitutional carry, and am of the opinion it’s how it oughta be.
No compromise.
At least not the ‘compromise’ the antis consider a compromise.
Absolutely. Provide state ammunition at cost for the live fire. I work in a “gun free zone” and can’t carry. Part of the problem with getting many of these regulations removed is that people are scared (irrationally, I know) about people who just might be armed around them being total f#@ktards. I think that basic demonstration of competence would help the existing statistics convince people that legal gun owners carrying doesn’t endanger them. I personally disagree with the “no compromise” stance because it makes it more unlikely that we will get rid of the most stupid and pointless gun regulations like gun free zones and suppressor and sbr restrictions.
Given that constitutional or permitless carry is a pipe dream for many states (e.g. New Jersey), should their courses have a mandatory live-fire component with the anti-gun agitprop propagators at the trace.org being the targets ?
I have mixed feelings. Sure I don’t “like” state mandates. I took the CHP class in VA, and while live fire is not required, the class was held at a range and it did include live fire. But before I took my class I took private lessons so that I wouldn’t look like a complete idiot. I was quite the newbie so shot with a Glock 17 to be sure I had the (easiest) weapon that I had learned with. Most people were fine, but one lady was truly scary. She had a .38 revolver, likely an LCR or Airweight. All in stainless steel and expensive. She simply could not handle it. Could barely load it. Could not hit within an 18″ circle at 3 yards. You could see the fear on her face, The instructor was patient and worked with her. I felt sorry for her, whether being sold the wrong handgun or just not being able to do it. I would not be surprised if she drives about as poorly as she shoots. And both of those make for scary situations.
If we simply trained every citizen in the use of simple arms then there would never be the ‘prove you can shoot’ infringement
Couldn’t some semblance of minimal competency be considered part of the “well regulated?” Or is my disdain for all things law, leading me to be obviously ignorant of something important?
Requiring state licenses to drive cars, is a pretty nasty imposition as well, but pretty darned common. And please, if anyone is even considering regurgitating the dum-dum-rah-rah that “driving is a privilege!”, please shoot yourself and get you over with.
The problem is, no one is trying from inside the state/DMV, to demonize and/or actively reduce the number of drivers/car-owners, as they are (and have been, for years) with shooters/gun-owners.
Once you give the authorities the means to require “reasonable” training, you have also given them the means to require UNreasonable training. Same with “reasonable” costs for permits/training, and “reasonable” restrictions on where a person can carry. It usually doesn’t happen right away; sometimes the first one or two administrators are actually serious about doing it in a right and reasonable manner. But eventually, the wrong person(s) will get in there, and then the screws will be applied; slowly at first, then increasing until more and more shooters/gun-owners are driven out, one or two at a time, until there is no longer a large enough community to effectively resist more draconian restrictions.
I hear you. As long as guns has been singled out as some great political issue, TPOTG are undoubtedly right to fight every attempt at increasing restrictions. But stripped the petty politicsation that permeates everything these days, in the abstract requiring some very basic minimal competency before being let out on the road with an 18 wheeler carrying dynamite, and/or a choice piece of field artillery, doesn’t sound obviously unconstitutional.
Requiring “training” is, as you point out, untenable, but requiring the ability to demonstrate a certain proficiency…..
The level of proficiency would obviously apply equally to absolutely everyone, from 4 star generals and El Prez’ secutity guards on down. Otherwise, it would simply be, as you say, a back door to further harass those not belonging to the more equals.
Please to note:
This map does have some errors, to wit:
Georgia does NOT require live Firing for a GA CC permit.
South Carolina DOES require live Firing for a SC CC permit.
Sow Kerlina DOES NOT RECIPROCATE my GA CC permit. The two State legislatures cannot come to an agreement on this after several years of trying.
As I do 80% of my business and travel in South Caklacky daily, I have installed a center console vault in my automobile in order to remain within the laws of the sovereign state of SC, but I cannot CC within the state.
Sneaking my carry gun into a hotel for an overnight stay? Do I carry it unconcealed through the lobby? If I stick it in my luggage, am I violating the CC non-reciprocity of SC law?
Not even a Utah CC permit helps me here….
I hoped from the title that the question was whether every citizen should be required to go through live-fire training, as a requirement for citizenship. My answer to that would be a rough “Yes!”
To the actual question: there’s a difference between the law requiring it and being able to find a course that doesn’t require it. In Oregon I have yet to meet an instructor who will teach a qualifying course who does not require life firing, so whether the law requires it becomes moot.
Comments are closed.