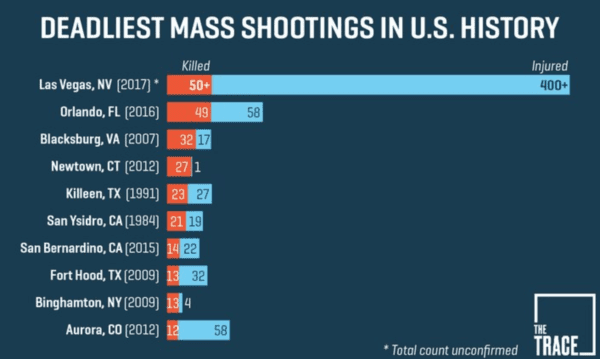
[UPDATE: In his latest news conference, Clark County Sheriff Joseph Lombardo said that the number of people killed by Stephen Paddock in Las Vegas has risen to 58 with 515 people wounded.] While the Las Vegas shooting is the worst mass shooting in modern American history, it’s not the worst ever, In 1890, the U.S. Cavalry opened fire on the Lakota tribe, killing somewhere between 150 and 300 members. FWIW, 25 soldiers also died at  the Wounded Knee Massacre.

RELATED ARTICLESMORE FROM AUTHOR

82 COMMENTS

  1. Paris, France: Bataclan (2015). 139 killed, 413 injured. Semi-auto and full auto firearms illegal in all of Europe.

      • Perhaps not illegal, but highly regulated and one needs a license to legally own, which attackers did not.

        • That is absurd. He would have passed any and all licensing requirements. Grow up and stop being reactionary

    • 139 dead, thousands held hostage to fear of heavily armed neighbors that night in France.

      Also known as any other Tuesday in the USA.

      • Actually known as every other Tuesday in Europe, nowadays.

        Fixed that for you. You’re welcome.

        • How far do you wish to go back in time to compare US and European violence? Twenty-five years to Europe’s last genocide in the Balkans? Or should we start our comparison around the mid-1930? Earlier?

      • How far do you wish to go back in time to compare US and European violence? Twenty-five years to Europe’s last genocide in the Balkans? Or should we start our comparison around the mid-1930? Earlier?

  3. Old white lone wolf terrorist attack. Can’t wait for the apologist to flock in.

    Let the panic buying ensue

    • The only “apologists” you see anywhere are those excusing or even defending — and quite vehemently at that — BLM, ANTIFA and their ilk. On the left.

      Not the other way around.

      Let the right-blaming ensure.

      • Please illustrate where those on “The Left” have defended private ownership of weapons used in this manner. A follow up explanation of severing the Militia clause from the Second Anachronism is then in order.

        Perhaps afterwards, when you finish your Ensure (with a Geritol chaser) you might explain how offering Credit where credit is due should not ensue – to those who’ve agitated for personal arsenals.

        Which of the concert attendees was tyrannizing the shooter, do you suppose.

        • Please illustrate where those on “The Left” have defended private ownership of weapons used in this manner. A follow up explanation of severing the Militia clause from the Second Anachronism is then in order.

          Here you go, since you oh-so-vehemently refuse to be informed about literally anything under the Sun whatsoever, in any manner whatsoever:

          https://townhall.com/columnists/johnhawkins/2017/06/15/20-liberal-calls-for-violence-against-conservatives-in-quotes-n2341401

          You even fill your articles with known, demonstrable, out-and-out lies to justify it, too.

          http://www.huffingtonpost.com/jesse-benn/sorry-liberals-a-violent-_b_10316186.html

          A follow-up explanation of why you seem to think that there has ever been a severing of the militia clause from the rest of the Second Amendment in the first place, which there hasn’t been, IS what’s actually in order.

          Perhaps after you’re finished reading that, when you finish changing your Depends, you might explain how blame-shifting of those who did absolutely nothing to encourage this — to those who’ve agitated for the confiscation of guns from people they don’t like.

          And, again, still nothing but known, demonstrable, out-and-out lies to justify all-out confiscation of property legally acquired and in good faith — and straight from the horse’s mouth, as it were.

          https://www.thedailybeast.com/yes-they-want-to-take-your-guns-away

          Which of the concert attendees, whose deaths that you leftists are in fact openly celebrating by the way, was tyrannizing your lot, do you suppose?

          Your snide, back-biting bile will be rightly thrown back into your face, which is exactly the only place it ever belonged to start with, unless and until you can actually develop the intellectual capacity the form cogent and coherent inquiries and arguments. You haven’t yet, and you damned-well KNOW that, too.

    • Sure.

      The fact he had enough rounds for a battalion is coincidence, right?

      Full auto and twenty rifles in a hotel room; what you’re on about is his Prozac.

      How many people medicated in America?

      Whatever helps you sleep at night, Snowflake.

      • How many people in America have tens of guns and tens of thousands of rounds to feed them? And they never kill anyone. It’s not important what you own. It’s about what’s going on in your head. In other words, it’s the guy, not the tool.

        • Bull-$hit. Lots of cranks, right here in River City.
          It’s the ones with an personal ammo dump mowing down the rest of us.

          This killer, like all the rest was law abiding until he slaughtered a conveniently assembled crowd of complete strangers.

          Which one of you heavily armed charm school graduates will be next?

        • @Naome Lixes — You’re bullshit. Lots of gangs, you mean, right there in River City.

          It’s actually the ones with the most drugs and turf at stake that are mowing down the rest of us, most all of the time.

          This killer, like most all of the rest, is not actually yet known to have been law-abiding or not to have had a long history of sever mental illness of some kind of another.

          Which one of you charm sk00l drop-outs living in your rich, Lilly-white, gated suburban compounds with hired armed security 24/7 ever know anything about anything?

      • Sure.

        The fact that he had enough rounds for a battalion, not that you would even know such requirements under any particular circumstance anyway, is moot and irrelevant.

        Valid and relevant inquiries into what made the man tick; you’re on about hardware.

        How many people have guns in America?

        Whatever helps you psychologically project at night, hypocrite.

        • None since he escaped from his village’s nut house. They need to come and claim their idiot before he trips and falls onto his own pitch fork.

  5. In Modern u.s. history. There were some really high death toll slaughters during the wild west. Mormons, unions, native americans….

  6. 5 of the 10 occurred during Saint Barack Obama’s time in the White House. I guess we know who’s really to blame for mass shootings, don’t we. (Hey, it makes as much factual sense as “the NRA did it,” and you know we’re going to be hearing that.)

  7. I’m expecting final death toll much closer to 100 once the dust settles. I think any chance of the share act going through just went flying out of the 32nd story window of the Mandalay bay.

  8. Five of the ten worst massacres happened during St. Obama’s tenure in the presidency…I guess we know who to blame for the scourge of mass shootings now, don’t we. (Hey, it makes as much logical sense as “the NRA did it.”)

    • Sure.

      Never mind that these shootings all followed the Supreme court nullification of the Militia clause.

      Getting hot in your crib, Snowflake.

      You lot own this one, and all the others.
      Congratulations.

      • Sure.

        Never mind that most of these shootings actually took place before the SCOTUS didn’t nullify the Militia Clause, which is something that you yourself demonstrated knowing less than absolutely nothing about, whatsoever.

        Getting hot in your diaper, Hypocrite.

        You lot own this one, all the ones before, and all the ones hereafter. Congratulations.

        Accept it. Get over it. Get used to it.

      • If I felt as threatened by gun owners (or as angry about them) as you do, I would pull up stakes and move somewhere more compatible. Most countries do not guarantee citizens’ right to keep and bear arms. Most countries have highly restrictive gun laws. You have many choices.

  9. Thanks, The Trace, for creating this wonderful scoreboard so future attackers know what they have to beat.

  10. The dead and wounded will likely closely match the number of dead and wounded in the Paris Nice attack. In which a truck was used.

  11. whenever a lot of pro gun stuff is going through congress or some anti gun president tries to sell his point something like this always seems to happen. as if it was staged, because the timing is always just right. it is like the “dems” make it happen so they can prove a point. and I do not put it passed them to do this sort of thing.

    • I suspect that there are very very few people who could stomach such a machination, under current conditions. They’d also get the needle (after 20 years in isolation) for that – That’s a hell of a risk.

      • Hinkley got a cushy cell and (later) supervised visits home. He almost got paroled.

        Useful tools of the evil POS (D) don’t just get tolerated, they get pampered.

    • What you’re experiencing is what psychologists refer to as frequency illusion. The classic example is when you buy a nee car, then suddenly you start seeing others with that car. There was no recent run on that make and model. You just notice it more because you just bought it.

      Similarly, you perceive spree shootings as being concomitant with pro-gun legislation, simply because you’re excited about and closely monitoring the progress of such legislation. Really, though, there are no connections. Ask yourself, what pro-gun legislation was in the works prior to the Sandy Hook, Batman theater, or Pulse night club shootings and got derailed because of it?

      • Persuading religious zealots to abandon their Faith never ends well. Full marks for the valiant attempt.

        • Especially when said religious zealots are ones who have merely substituted some “magic man in the sky” with the government instead, and elevated it to the level of a god-thing in “his” place.

          Zealots like you.

      • The point of the story is it took a regiment in South Fukota what it took only one shooter in Las Vegas. Nice attempt at mitigation of the latest obscenity.

        Progress.

        • The actual point of the story is that the latest obscenity is not (strictly) the deadliest massacre to occur on U.S. soil. Nice attempt at summarily dismissing a point that you know full-well that you can’t refute.

          Same as it ever was.

  13. Cut the conspiracy bs. No mass shooter has ever been shown to be motivated to do it for gun control. Theres always firearms bills working through our federal and state govts. There are always mass shootings occuring. Correlation is not causation.if u wanna talk false flag infowars is your site.

    • If you wanna dismiss the possibility of a false flag out of hand then CNN is your news outlet…

    • Such plots have existed in history. They’re unlikely, exremely so, in any given incident, but they aren’t impossible.

      I didn’t believe the ATF’s Fast and Furious scandal was what it was at first. I thought was just Internet kook talk, until the proof came out. I think that Sandy Hook deniers are kooks, because there’s no proof.

      I’m not saying this L.V. incident is anything more or different from how it currently appears. I’m just saying that not everything that happens is necessarily as it appears.

      • The SSL certificate for the first and largest of the Sandy Hook memorial web sites was purchased 3 days before the event took place. SSL certificates can’t be spoofed. It is NOT proof that nothing happened at Sandy Hook, but it IS proof that it was a planned event. It is also PROOF that NOTHING you hear on the news or from your government can be trusted. There’s always a grain of truth, but twisted, manipulated and blown out of proportion, always to suit an agenda. The agenda is simple: more power.

    • I suggest reading up on the Wounded Knee Massacre Robert points to. The motivation for the slaughter was the enforcement of gun control on a historically disadvantaged community.

  14. The headline is very deceiving. While true for MODERN history. These examples are far from the most deadly in U.S. history. Unfortunately the tabloid media of today cares not about facts. Only about sales,clicks and ratings. People have been slaughtered and massacred in not only this country but around the world since the dawn of Mankind, The instrument of those killings has changed over the centuries. Only in the last 40 years has the blame been given to the choice of weapon instead of the person. Democrats/Liberals have had the power to legislate gun control many times during these years. As with many other of their so-called concerns they have only used that concern as a talking point for election. They have tried to subvert the 1 true law of our nation (the Constitution) many times with the courts and failed. I do not believe they truly want change. For without chaos they have nothing to show their concern for. Keep Your Powder Dry…

  15. How long until we get the breakdown between people who were injured or killed by gunfire and people who were injured or killed in the resultant stampede? Will The Trace’s leaderboard be adjusted accordingly?

    • Doesn’t matter, really, as those deaths were the result of people trying to escape the gunfire. I am curious, though, how many were shot vs. killed in the ensuing melee and wonder if that will come out or not.

  16. The news outlets have already picked up on slide fire stocks. Look for those to receive the ATF ban hammer by the end of the week if they were used in this shooting.

  17. They have to use the phase “mass shooting” because if they used the phrase “mass murder,” they’d run up against al Qaeda and September 11, 2001. Can’t risk reminding people of that.

  18. Very poor comparison. If you’re going to use military actions you might as well include Civil War battles in your “statistics”.

  19. The formula is predictable. Announce the latest score compared to the last several shootings, then parade a bunch of politicians, celebrities, and layman reactions (essentially the most uninformed lot they can find) and trumpet whatever gun violence/control agenda using as many politically correct buzzwords as possible while ignoring all logic and facts.

    Full retard.

  20. I think it’s fair to call the Colfax Massacre a mass shooting. Somewhere between 60 and 150 African Americans were murdered.

  21. COMMON SENSE GUN LAWS THAT COULD HELP PREVENT MASS SHOOTINGS.

    The insane blood and carnage on mass shootings must be brought under control and failure to adopt any new laws only guarantees the mass murder will go on and on.

    Here are some Common sense gun laws that would help prevent mass shootings. Most have been adopted by civilized Industrial Countries many decades ago and they have for the most part worked a majority of the time. Although there is no panacea for foreign government sponsored terrorism.

    1. Mandatory Psychological testing of all gun purchasers. Issue of a gun owners permit to buy.

    2. Mandatory vetting of all gun purchases even between individuals and transfers only through licensed dealers.

    3. Mandatory use of safes for secure storage of firearms which would prevent not only thefts but child accidental shootings.

    4. Mandatory security alarm systems

    5. Severe restrictions on magazine capacity for assault rifles.. These weapons are far more deadly than pistols and their extreme deadly long range make it mandatory that high capacity magazines should be outlawed all together. The recent mass murder by a man on the 34th floor has shown the extreme deadliness of the rifle as compared to the pistol.

    The U.S. is no longer a Colonial Country of only 3 million people but one of over 300 million people and the old outdated idea that the Second Amendment was written for unrestricted use of firearms shows how outdated our Constitutional System often is by making it almost impossible to adopt laws that are in dire need of 21st Century America. It has been shown that over population not only creates more mentally ill people but it increases all out of proportion to the actual numerical increase in numbers of people. In other words a 50 per cent increase in population does not increase the mentally ill by 50 per cent but often at a far higher percentage rate. Studies done as long as 5 decades ago proved this point.

    Failure to provide affordable mental health care has also increased mass murder in the U.S. as well. The U.S. has spent and continues to spend over 53 per cent of its tax revenue on senseless wars of rape, pillage and conquest to enhance the wealth of the filthy rich rather than spend the tax dollars on social programs that provide free education, health care and prescription drug coverage. The U.S. has become less and less a desirable place to live in the current 21st Century Industrialized World as compared to much more Socially Advanced Industrialized Nations. It is not surprising to note that Immigrants and Refugees often prefer other countries to immigrate to instead of the U.S. that in past years was quite the opposite. Even foreign people have now come to view the U.S. as a lawless, and Cruel Capilalvanian country. When even some poor African Countries have lower infant mortality rates than the U.S. does it is a wake up call to anyone contemplating coming here to work or live and to the Americans that must go trying to survive in a country that seems to be coming apart at the seems.

    I think too the new insane proposal of cancelling the old severe vetting of silencer purchases is now dead on arrival as it certainly should be. Even with the loud noise of the current mass killing it took awhile before people realized they were hearing gun shots and if the nut case had had a silencer it would have taken them even longer and the direction of the gun fire would have been more difficult to detect by the police as well. As one can see taking off severe vetting of silencers is so insane it defies all common sense.

    • And yet, you can buy suppressors over the counter in places like New Zealand. Nothing controversial about it.

      I’ll let others deliver the thrashing these asinine recommendations have coming. It’s well worn material for me. Besides, others who have only recently come to embrace their human right to armed self-defense could use the practice refuting such arguments.

    • 1. Counterpoint: poll tests. “Testing” for the ability to exercise a right invariably ends in disenfranchisement. Enough said.
      2. Violation of Fourth Amendment. An individual’s property is theirs to control, not the government’s. Besides, de facto violation of FOPA by creating a “registry”.
      3. Unenforcable and would introduce another regulatory and financial burden on all law-abiding prospective owners. What are the cops going to do, go around and perform mandatory inspections on every gun-owners safe? You need warrants for that, and for warrants you need evidence a crime was committed.
      4. Mandatory security alarms? What? What sort of place do you live where everyone has the money to pay for alarm systems and monitoring?
      5. For heaven’s sake. No. “Assault rifles” are not “far more deadly than pistols” nor do they have “extreme deadly long range”. Look up the FBI crime stats and report back with what percentage of crimes involve a rifle of any sort. Hint: it’s very, very low. So low, in fact, that slippery restrooms claim more lives every year than criminals with rifles.

      A fine point: military expenditure is around 30 percent, not 53. The majority of that money goes to servicemembers in the form of active duty pay, pensions, and health care.

      And, for what it’s worth, silencers are not “severely vetted”. They go through the same background checks as any firearm purchase. The only difference is that there’s an outdated, needlessly-lengthy regulatory process with a punitive tax stamp. This is 2017. There’s no need to pretend the poor don’t deserve the same rights the rich do.

      • The tax stamp isn’t meant to be punitive. It’s meant to be confiscatory, as in stealing or extortion.

        • Spare us the Libertarian Theology.

          Gun owners should be underwriting the cost of intentional misuse of firearms.

          Bullets are cheap.

        • Truck owners should be underwriting the cost of intentional misuse of trucks.

          Bullets are definitely not cheap. That’s why I cast my own. Cartridges are even more expensive. But you wouldn’t know what’s the difference.

        • @Naome Lixes — You actually need to spare us the Communist Theology.

          Gun control advocates should actually be underwriting the cost of the international misuse of guns.

          Mass graves and cremations are what’s cheap.

    • So basically the same restrictions that prevented the Bataclan massacre?

      Bureaucrat: n. 1. One who, upon learning that his neighbor has killed his entire family and then himself, is most upset that he never got it approved by the Planning Committee first.

    • * 1. Mandatory Psychological testing of all gun purchasers. Issue of a gun owners permit to buy.

      What other rights are we going to put behind a competence wall? Voting? Having babies? Speaking in public? Who decides whether someone is competent or not?

      * 2. Mandatory vetting of all gun purchases even between individuals and transfers only through licensed dealers.

      Private transactions between citizens are no business of the government. Not to mention that this is, as has been shown where it has been implemented, utterly unenforceable without a national registry of firearms, which is explicitly illegal.

      * 3. Mandatory use of safes for secure storage of firearms which would prevent not only thefts but child accidental shootings.

      So who will verify this? Now owning a gun makes you give up your right to privacy, to UK-style surprise inspections of your home?

      * 4. Mandatory security alarm systems

      ???

      * 5. Severe restrictions on magazine capacity for assault rifles.. These weapons are far more deadly than pistols and their extreme deadly long range make it mandatory that high capacity magazines should be outlawed all together. The recent mass murder by a man on the 34th floor has shown the extreme deadliness of the rifle as compared to the pistol.

      Yet all rifles in general account for a tiny percentage of all firearms related murders. Not to mention that a criminal who has no regard for the consequences of fucking murdering 56 people will also not blink at the consequences of being caught with an illegal-capacity magazine.

    • “The U.S. has become less and less a desirable place to live in the current 21st Century Industrialized World as compared to much more Socially Advanced Industrialized Nations.”

      you mean “Vast Majority White Monoculture Socialist Authoritarian Western European Nations”, you racist.

      • Perhaps a clarification is in order: America is far more dangerous than other Nations outside of War Zones with functional governance, safe tap water and transportation that doesn’t require donkeys.

        • An actual point of clarification is in order: America is far safer and has been getting steadily safer, seemingly despite the proliferation of guns and concealed-carry permits, for the better part of the last quarter-century. You literally cannot say that for almost anyone else without making yourself a liar.

  22. Here in Brazil we do not, in fact, live in jungles, having the sixth Greatest GDP in the world by 2012, tho incompetent politics tanked it to 9th or so.

    The reason I’m saying this is to out in context that we aren’t some desolate African nation.

    And you wanna know what’s our average DAILY death toll, murders only? 165. That’s right, around three Las Vegases every. Single. Day.

    You guys can guess about how free we are to own firearms.

    I dearly hope one day we are as safe and free as the U.S.

  23. Indian wars don’t count. Might as well count the Civil War. FWIW this mass shooting probably won’t have as big of a negative affect as Newtown. I hope…😡

Comments are closed.