Back in November, TTAG ran a post about a Black Friday “doorbuster” sale at Dick’s Sporting Goods. They were offering a Remington 700 ADL Varmint for $350.00. As it turned out, I just so happened to be in the AO about a ½ hour before midnight when the sale started so at the last second I decided to partake in the Black Friday madness. For reasons still unknown to me, I picked up one of these “doorbuster” 700s, and after putting 200 rounds through the rifle I can report to the Armed Intelligentsia . . .
In the interest of laziness, I’ll assume the reader is already familiar with the basic workings of a Remington 700, since over 5 million of them have been produced. Rather than rehash the basics or give you a history lesson on the evolution of the design, my goal here is to simply give you an unbiased, critical assessment of the specific features of the package offered by Dick’s, as well as a little G2 on its accuracy, fit, and function. I’ll also tell you some details on the Nikon Coyote Special scope that now adorns the rifle. Let’s get started.
The Dick’s Sporting Goods 700 ADL Varmint is an exclusive package consisting of an “ADL” version of the 700 SPS Varmint and a crappy scope (not shown in above photos). The distinguishing feature of an ADL rifle is the internal (aka “blind”) box magazine, which lacks a hinged floorplate on the bottom of the rifle. ADL stands for “A Deluxe,” and was Remington’s “no frills” economy line until it was discontinued in 2004. From what I understand, Remington now only produces ADL rifles as special runs for the various big box stores, etc.
Despite the fact that the ADL is the low-end of the production line, I was hopeful that I might still score a decent rifle for cheap. My fellow TTAG writer Chris Dumm has a skinny-barrelled Remmy ADL in .270 Win that he picked up for $250, and I have watched him shoot a ¾ inch group at 300 yards with that rifle using cheap Wally World ammo.
The rifle features a full-floated 26-inch heavy contour barrel (.820 in. at the muzzle) and a polymer stock with vented beavertail fore-end. The stock is finished in Mossy Oak™ “Brush” camouflage and the the Remmy weighs in at 8½ lbs, most of it in the barrel.
Dick’s offers this rifle in .223 Rem, .22-250 Rem, .243 Win, and .308 Win and I went with a .22-250 Rem. Why? Well, I already have a good TC Icon in .243 Win. and some super-nice precision rifles in .308 Win. I don’t think the .223 Rem. benefits much from a 26” barrel. And the .22-250 Rem has a reputation as being a very flat shooting round that can zip out of the muzzle at 4000 feet per second.
I admit that the .22-250 isn’t the most versatile of the calibers that Dick’s was hawking. The .308 would be a great low-price tactical precision rifle or big-game gun, and the .243 would excel at anything from groundhogs to deer and antelope. The .223 version would do most of what the .22-250 does, but it would do it with cheaper and (until last month) more available ammo. Let’s face it, a 26″ barreled .22-250 is built for just two things: target shooting and varmint hunting.
There’s a downside to .22-250, though, and that’s that it will often toast a barrel in just a few thousand rounds, especially if you shoot the fast loads. But a Remington 700 action can be rebarreled fairly easily, so it’s not the end of the world if and when that happens. Besides, even if it only lasts 2500 rounds, that’s a lot of dead coyotes!
PETA types routinely soil their diapers over any type of hunting, but their hysteria is completely illogical when you think about it. Coyotes typically end their lives in starvation, hypothermia, or the gnashing jaws of other predators. And rodent varmints face the additional horrors of Bubonic plague and hemorrhagic fever. The instantaneous explosive deprogramming of a 4,000 fps .22-250 bullet is a swift and merciful deliverance, compared to these grim and grisly fates. Considered in that light, popping a squeaker with a .22-250 is one of the most “ethical” things you can do for the poor creature. Or so I justify it, anyway. I figure God put those things on this earth to be targets.
One thing that really attracted me to this rifle is the Mossy Oak™ “Brush” camo stock. It’s a very effective pattern for the central Oregon high desert scrub lands in which I hunt coyote. Maybe it’s the military guy in me, but I like my camo to match my duds. So to have a gun that coordinates with my camo huntin’ clothes, well . . . that frickin’ cool. You gotta be fashionable when out in the bush; you never know who you’ll run into out there in the high desert. At some point, I’m gonna have to Duracoat® the barrel, action, ARD, and Harris bipod in coyote brown and desert tan to match.
Remington does a pretty good job on these stocks, all things considered. They lack the aluminum bedding system featured on the HS Precision stock that came with my 700 PSS. As a result, I figured that such a cheap stock would have a negative effect on accuracy. I expected I’d eventually need to replace it with a Manners, McMillan, or Bell & Carlson stock if I wanted to get really fine accuracy. But this gun shoots so well with the factory stock I don’t think it really needs to be upgraded. That’s just fine with me, because I doubt I could find an aftermarket stock in that same Mossy Oak™ camo pattern in any event.
The trigger guard is made out of plastic, but that seems to be the way of the world these days. Sigh.
Update (October 2014). Sure enough, it didn’t take long for that crappy plastic trigger guard to break. POS.
And speaking of personal preferences, I really prefer detachable box magazines. Given that even a hinged floorplate makes me feel like I’m slummin’ it, it should come as no surprise that I think the ADL set-up is pure ghetto: the worst-of-the-worst arrangement. I hate it and here’s why: you have to really pay attention when you load an ADL, because any mistakes in how you load the rounds will cause the gun to jam. Trust me on this one. And it’s difficult to load with gloves on, especially if you are situated in a shooting position. Unlike a BDL, you can’t easily fix the mess by dumping the mag out the bottom. But, for $350, beggars can’t really be choosers, eh? So be it. Just pay close attention when you load ‘er up and you will be good to go.
If you’re familiar with the Remington 700’s action, this “economy” version offers no surprises. The action is noticeably less smooth and refined than a Remington Custom shop 40-X, but I think it’s only slightly less smooth than the 700 PSS and other “mid-range” 700s. It certainly doesn’t feel rough, or overly cheap like some entry-level guns.
The triggers that come on modern hunting rifles are sweet. Seems like thirty years ago, the gun manufacturers made their factory triggers suck on purpose. It was almost as if gunsmiths around the country were giving kickbacks to the gun makers to ensure that the ‘smiths would get the extra business.More realistically, I think the product liability lawyers were the real culprit.
But times have changed, and these days it seems as if the standard for triggers is set pretty high. Guns are rolling out of the major factories with excellent triggers that don’t typically need extra work. This gun features the “low-end” version of the new X-Mark trigger, which isn’t intended to be adjustable by the consumer. But honestly, I see no need to have a ‘smith adjust this trigger, nor do I see any need for an aftermarket unit from Jewell, Timney, or Rifle Basix. The factory trigger breaks at approximately 5 lbs. and has no creep or overtravel. I’m very impressed, especially considering its price point.
At the end of the day, a bolt gun with a long bull barrel is really only intended to do one thing really well, and that is to allow the shooter to fire lots of bullets into small groups at long range. So does the 700 ADL Varmint deliver? Yes, yes it does – in spades. In fact, this rifle shoots sub MOA all day long. It especially likes the 45 grain Winchester JHP Varmint loads (4000 fps), which consistently fired ½ inch or smaller groups. My personal best with the rifle so far is a .39 inch group using Wally World Winchester White Box. Using Hornady’s 55 grain V-Max (3680 fps), my groups seemed to average in the .6 to .8 inch group range though I did manage to shoot one 3-shot, .44 inch group with it
Update (October 2014): This rifle has proven to be highly accurate in the field as well. I have taken it on two “squeakie” (Belding Ground Squirrel) shooting trips, which are high volume affairs where the barrels get hot! I averaged 100+ rounds on both trips and accuracy has been consistently high (roughly 1/2 MOA +/-). Recently, I shot a 1 inch group on steel at 300 yards using Winchester 55 grain ammo. I also took out a coyote at 623 yards. At least in field conditions, this seems to be the outer limit of this rifle’s capability. I really like how fast the bullet gets to the target!
The fact that the barrel has a 1:14 twist rate does limit the type of ammo you can shoot out of this rifle. Some of the 60 grain factory loads may exceed the limits of the rifle. Certainly, anything over 60 grains will be a no go.
The Scope, Bases, and Rings
The 4 x 12 scope that comes with the Dick’s Sporting Goods package is branded with the Remington name. Remington does not, to my knowledge, actually manufacture scopes. Although this scope is shown on the Remington website mounted on a few 700 models, no information is provided on the scope on the website. It appears to be some sort of cheap, no-name, made-in-China optic. Tasco maybe? Who knows. It feels pretty solid, but I tested it out and found it to be marginal at best. At both 50 and 100 yards, I couldn’t get the reticle and the background to be in focus at the same time: it was a one-or-the-other deal. I still managed to shoot a few ½ to ¾ MOA groups with the scope, so I guess it would do in a pinch. But it wasn’t ideal by any stretch of the imagination.
The two-piece aluminum scope mounts that came with the guns are from Leupold’s “Rifleman” series which is their “economy” line made in Singapore. These mounts retail for $10. Normally I prefer one-piece scope mounts due to the better alignment they achieve, but with the ADL I want as much room to access the magazine and chamber as possible. There isn’t a whole lot else to say about the mounts; they seem to work well, and I don’t see any need to replace them.
The scope rings that come with the rifle, on the other hand, appear to be extremely cheap. I am not exactly sure who makes them, but I’ve seen identical rings marketed under the Simmons brand name, retailing for less than $8. But the rings do not appear on the Simmons website or catalog, so I can’t be sure as to their origins.
I’m certain, however, that the rings need to be replaced with something more rugged. There is no way I’m going to have a hunt ruined by an $8 pair of rings, when I can get a decent set for $30-50.
The Nikon 4.5 x 14 x 40mm “Coyote Special” scope seemed like the perfect optic for this gun, especially when mated with matching Nikon (Warne) scope rings. I’ve seen the same Warne rings in black sell for $30, so you pay a hefty premium to get the Mossy Oak camo version, but hey, I gotta match, right?
This scope originates from Nikon’s popular “Buckmaster” line, which is their mid-range offering. It focuses in the second focal plane and gives a respectable 92% light transmission, which is comparable to the Leupold VX 1 and VX 2s. I also appreciate the side parallax adjustment as well. Overall, it’s an impressive scope for the asking price ($299.00 on sale at Cabela’s).
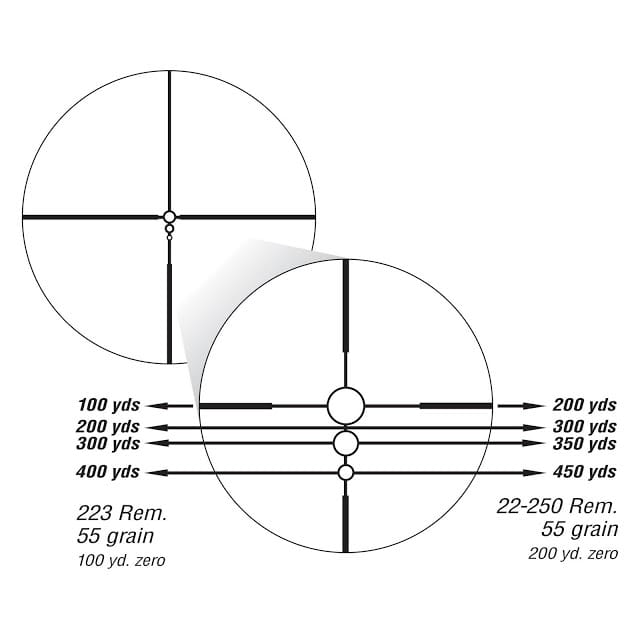
It is worth mentioning that for most people, Nikon’s BCD reticle is either going to be a love-it-or-hate-it affair. According to Nikon, the “unique, open circle design doesn’t obscure the target, making shots on a moving coyote simple.” Well, that’s true for the most part. Obviously, you will experience some variation in trajectory for every different load. Plus, even assuming your bullet matches the “design specs” of the reticle, if you have to take the shot at 300 yards or 400 yards, then you have to aim in between the circles, which is a bit odd. I have not taken a shot yet at those distances, so for me the verdict is still out on this reticle. Given that the .22-250 will shoot Point Blank Range to over 200 yards, you will not likely even need to worry about using the bottom two circles in most instances.
At 100 yards, the largest circle (i.e. the one in the middle of the reticle) measures 3 inches when the scope is set to 14x. In the top photo, above, I tried to show how the reticle appears on a 100 yard target at 14x. For reference, the red circles on the Sight Bright™ target are two inches in diameter. In the bottom photo I dialed back the power setting to 4.5x and took another photo. The reticle’s top circle covers approximately 8 inches at 100 yards when set to 4.5x. I initially thought that this reticle design would make it difficult to shoot precise groups on paper targets, but I found it to be quite easy, especially when shooting at circular targets. After all, it’s pretty easy to line up a circle in a circle. In fact, I shot a few .4 MOA groups at 100 yards with the scope set to 4.5x.
It occurred to me that with a little effort, it would be possible to use the three circles for range estimation, in the same manner as a mil-dot reticle. Although it would probably take an afternoon of testing at the range to work out and tests the charts, Nikon could do its users a service by posting this type of info on their website.
The Coyote Special scope comes with an “ARD” device, which is a screw-on honeycomb grid filter that prevents sunlight from reflecting off the front glass. BTW, “ARD” stands for “anti-reflective device.” Originating from the military, these devices are a “tacticool” alternative to barrel-style sun-shades. However, they do have the downside of somewhat decreasing the amount of light that’s transmitted through the optic. The reduction is definitely noticeable, especially in low light situations.
Parting Thoughts on Dick’s “Black Friday” Sales
Overall, I’m really happy with the Remington 700 ADL Varmint. Was it worth going through the Black Friday sales experience just to save a $100.00? Honestly, no. I arrived on the scene at 11:30, and the doors opened a few minutes before midnight. I ended up being the second guy in line at the gun counter. The sales staff were friendly and personable, but it was pretty clear that the store wasn’t really set up to handle the deluge of customers. Even though I was second in line, it took over an hour to complete the purchase.
Not only that, but Dicks made you pay for the gun that night, even though you had to come pick up the gun later the next day. WTF? In any event, I’d have thought that they would have had the background check completed by the time I came back two days later, but I ended up having to wait around for over another hour to get that done. Overall, I thought the experience was a complete Charlie Foxtrot. Although I’m glad I tried out the “sport” of the Black Friday shopping experience, I can honestly say I wouldn’t do it again.
Specifications:
Caliber: .22-250. Also available in .223 Rem, .243 Win, and .308 Win.
Barrel: 26 inches, with a 1 in 14 right hand twist.
Length: 46 & 1/2 inches
Weight: 8 &1/2 lbs. empty.
Operation: Bolt action.
Metal Finish: matt black oxide finish.
Capacity: 4 +1, internal box magazine.
Price: Typical street price for 700 ADL Varmint is in the $550.00 range, but it is commonly seen on sale at Dick’s for $450.00 to $475.00. Dick’s 2012 “Black Friday” doorbuster price was $449.99 plus $100 factory rebate (net: $349.99).
Ratings (Out of Five Stars):
Accuracy: * * * * *
Can’t beat the accuracy (½ MOA with some factory loads) for the price.
Ergonomics: * * * *
Although a little muzzle heavy, the stock is very comfortable. I’ll take a one point reduction for that annoying 90° bolt throw.
Reliability: * * *
The ADL’s internal blind magazines are easy to jam up if you don’t exercise care when loading. Be sure to have a visual on the breech when feeding this model.
Durability: * * * *
The Remington 700 series of rifles is generally not failure prone, but I will deduct a point for the crappy plastic trigger guard: 4 points.
Customization: * * * * *
This is probably the best reason to go with a Remmy 700 over any other brand: tons of aftermarket parts and accessories.
Overall Rating: * * * *
In this price range, there isn’t much competition out there. The Savage Axis series is closest. Although I’m a huge fan of the Thompson Center Venture Predator line, the price of the Remmy comes in two to three bills cheaper.


















Actually, this makes me feel better about missing out on getting a .308 that day. I arrived at a little after 0800 at Dick in Fairfax. The line was out the door and all they had left were .223’s and a few of these reviewed here. For $350, getting a budget .308 that has feed problems and a crappy scope would have felt disapointing. Plus I am NOT big on moss oak or other camo pattern stocks.
Excellent write up. Thanks for reviewing it.
I wouldn’t necessarily say that the that the Remmy 700 ADL has feeding “problems.” It does, after all, work as intended. Its just harder to load than a box magazine, esp. if you are in your shooting stance and you try to load the rifle without looking at the chamber. Given that this is primarily a hunting rifle, I don’t think that it THAT big of a deal – in most cases you will be loading the magazine before you get to your stand in otrder to minimize movement and noise.
You wont get a better rifle for the price……ever.
I wouldn’t say that. I happen to see some K31s for about $200 a few years ago that were more than capable, plus they have detachable magazines.
I love me some Karabiner Model 31 (K-31). I have 4 of em that I got in the 2005-06 time frame, $100 each at Big 5. I’m guessing that new ones would cost 2K if they were made today. All are MOA capable using surplus Swiss ammo.
That’s a familiar-looking rifle. Thanks for the writeup. It’s nice to hear about my gun from someone who knows more about them than I do. I know it currently shoots better than me, but I didn’t know how well it was capable of shooting, so I’m happy to see what you found.
I’m still using the stock scope, rings, and mounts, and yours are much nicer. Matching is important! I knew the rings were bad when I saw that the “clamping side” was a piece of bent steel rather than a block of aluminum. I had the rings on and off about 3x before I was satisfied, and each time I was able to tighten the screw about 1/8 turn further before it was “tight.” I used a scope mounting kit (the kind with the fat bars with the pointy ends that are supposed to line up) and they were pretty far off, so I ended up swapping the ring tops and turning them around in about 5 different configurations before they got close, and then I lapped them down ’til they were perfect. The rings are definitely high on the “replace soon” list.
Your comment about “bull barrel… lots of bullets” leads me to a question. On my first (and so far only) range trip with this rifle, I put my last 8-10 rounds down the barrel in pretty quick succession (maybe over 4-5 minutes), as the last range session was wrapping up and I got a little silly. Naturally accuracy (probably much more mine than the gun’s) suffered as a result. When I was done, the barrel was too hot to touch for easily 10+ minutes. I realize I was basically burning money at that point, and probably won’t do that again, but realistically, how many rounds in rapid succession does it take for the rifle’s accuracy to really suffer with that bull barrel? Mine’s in .243 Win if it matters.
I’m interested in the answer to the barrel-life question as well. Perhaps Dyspeptic will make an appearance later today to enlighten us.
While I like the ballistics of the the 22-250, I really don’t like the idea of a barrel life of only a couple thousand rounds. I’m a big believer in buying the best I can afford and keeping it for the long term, and the idea of a barrel which would only last 5-10 years before replacement just doesn’t seem attractive.
Then again, we ARE talking about a sub-$500 gun, so maybe it’s better to think of these as consumable items instead of durable goods…
I have owned 6 22-250 rem rifles. First and favorite go to is a 24′ barrel Savage 10. I had to replace the barrel at just over 1800 rds. Im OCD about round count. I blame my dad and 30 yrs in the Military. Now I don’t reload for 110% max loads BUT, I load them fast. 55-60 gr Amax mostly and Hollow points. To say they are critter slayers is a gross understatement. Hope this helps. on average factory copied load performance I would assure you 1900rds is feasible.
Jim
Also, Matt, you should invest in at least a few gunsmithing screwdrivers. Craftsman wedge-shaped screwdrivers will be the death of the screws on your firearms. Ask me how I learned this. :\
Heh, thanks. By gunsmithing screwdrivers, I assume you mean some that have a tip profile like |_| instead of \_/, right?
In this case the big one was for the massive thumbscrews that held the ring bases to the rail, and the little one was just for removing the little studs that were in the threaded receiver holes, so that won’t be an issue again. (Incidentally, is there any reason to keep those little studs? It’s not likely that this rifle will ever have the scope mounts removed permanently.)
Close. Check out the hollow-ground vs conventional tip diagram partway down this page:
http://www.core77.com/blog/object_culture/apples_custom_screw_hullabaloo_hollow-ground_bits_and_why_a_vintage_sewing_machine_repair_brought_me_to_the_gunsmiths_18355.asp
Every machined product I own, especially firearms, has its own large zip-lock bag in my parts storage boxes with all of the “leftover” stuff, including filler screws like the ones from the mounting holes. Tiny stuff like those screws get their own small bag. It’s come in handy enough for me to make it a standard practice.
That’s also where I keep the original receipt, manuals, and other useless stuff that suddenly comes in handy if you ever want to sell or give that equipment to someone.
I really don’t know the answer to your question, But I was always taught that letting the barrels get really hot negatively affects the life of the barrel somewhat. That could be an old wives tale for all I know, but it seems to make some sense. I will try to do some tests the next time I take the gun to the range (assuming I can find more ammo for the dang thing!) I feel pretty sure that you could run a box or two of ammo through the bull barrel in a fairly rapid manner without any significant POI shift. My HK 93, on the other hand, has a skinny barrel, and it will experience a noticeable POI shift after 30 round of 5.56 fired at 1-2 second intervals. Shot number thirty will be an 1 & 1/2 inches high and slightly to the left!
Just out of curiosity, what kind of groups are you getting, and what ammo are you using? .243 Win comes in a wide variety of bullet weights, from little 52 grainers up to 100 grain or so. By guess is that your rifle will shoot some bullet weights better than others.
I only had time to put a little over 30 rounds through it on my only range trip so far. That was a box of Remington Core-Lokt and a half box of Win Super-X, both in 100 grain. As Michael said below, it took me about half the box of Remington to get it sighted in, and I ran through the last half dozen, so only about 15 “fire for effect” rounds. In that, I could pretty consistently put 3 rounds in 3/4″ or less, but the fourth and fifth would always be another 1/2″ or more out. I was slow-firing, so I know it was me, not the gun. It’s clearly capable of better than me at this point.
I’ve got some 80 grain and some 55 grain, so I’m going to try to make an effort to get to a range in the next couple weeks and allow more time on this trip.
I got the same in .223 on Black Friday from Dicks…I would have taken a rain check on the .308s but the guy at the desk couldn’t figure out how to make that happen…he was otherwise helpful.
Dick’s made me fill out a number of release forms aside from the standard ATF form, I didn’t care for that.
Haven’t shot the rifle yet, but trigger does dry-fire very nice.
And here you thought you were making a good decision because it shoots some of the most commonly available rifle ammo on the planet. 🙂
Bastards. I missed the last ones at my local Dick’s by ten minutes. 🙁
Good stuff. One of these days I’m going to get a bolt-action rifle, and my income being what it is, I’ll be buying at the bottom end of the market. This one’s going on the short list.
Glad to hear you got a great deal. I am always weary of low cost firearms from well known companies like Remington..for no logical reason, I have this stupid feeling that because it’s cheap it was not well made or designed carefully like the other “better” weapons in their line-up. I know there are different features and even different manufacturing technique, they probably have just as good engineering as everything else. I need to be more open minded and I appreciate reviews like these. Good info, thanks.
OH no to Obama’s military brainless buddy McCristal that .223 rifle is a too powerful sniper rifle for those poor varmints….. Get a .50 BMG Barret instead!!!!!!
I got a .308 version of the same for a basic whitetail hunting rifle – I’ve been quite happy with it; it has been out about 3 times now and put one doe in the freezer last month. It took almost a box of ammo to get the included scope on zero, and another half a box to get comfortable with it. It’s more accurate than me, for now. I’ll eventually buy nice glass but the freebie works, although it is blurry.
Dick’s was a PITA. I’m still waiting on the $100 MIR to come back, but I did haggle an extra $40 off at point-of-sale, basically negating sales tax, because I had already been to the store twice to try to complete the sale. I had to go back a third time to get the correct forms for the MIR. They couldn’t run NICS or take payment during the Black Friday sale, etc. If the rebate ever comes back, I’ll have $346.88 in this gun – and that to me is a fair price for a hunting rifle that can take a beating for years, and a solid platform for future upgrades should I ever desire.
I got one of these in .308 at midnight on black Friday:
https://picasaweb.google.com/lh/photo/Kapq9vd7HhBTZcC3wKgmcBEuTXilBpsBld6HwyXqFXE?feat=directlink
Still haven’t gotten my rebate yet.
The rifle shoots well – probably better than I do. Using the crappy scope at 300 yards I was able to get my shots to land in my friend’s spinner frame, but I couldn’t see the target well enough to hit the 3″ spinner.
100-200 yards was no problem with the included scope.
New glass is a must for this rifle. I think a new Leupold might be on the list for the next birthday.
The rebate said 8-10 weeks. You should have gotten an email by now, if you sent it in right after purchase. Hell, I waited a week and I still got my email on 12/27. There is a website where you can check your status on the form, and in the email.
Just checked – rebate is on its way!
Thanks!
A word about the Nikon BDC Reticle and how it works: in a nutshell, if you have the time to plan and take your shot while estimating your range and figuring out which part of the circle or in between to hold over, then fantastic. In reality, you won’t have the time.
Perhaps I was doing something wrong or not doing it right, but what you do is once you have the Nikon scope mounted with the BDC reticle on your rifle of choice, you can use their BDC software to tailor your exact round, caliber, etc. to the reticle, and once you know where your rifle is zeroed (200 yards for example), then you can plug in some number and voila – print out ballistics sheet (hold over points for that load at various ranges – generally 200 yards to say 600 yards) that can be taped to the inside of a scope cover – which is what I did – except I had to do it 3 times. Yep, 3 small ballistics tables for my load showing the hold overs FOR 3 DIFFERENT MAGNIFICATIONS (4.5x, 9x, and 14x). Yes, Sir. You change the magnification on your variable power scope and that changes the point of impact for each circle – top, middle and bottom. The change could be as high as a 50 yard difference and unless you overcome your buck fever and can memorize all of the hold overs, then you are basically back to a sort of Kentucky Hold Over/Guesstimation.
It is not a bad set up, but I think it benefits precision shooters who can take their time before they shoot. Regardless of what game animal it is, you probably won’t have the time to range, check the ballistics table, double check the magnification in relation to the table, breath, and then shoot.
Just my two cents on that – it is what it is. I like to generally know where my hold over is and running it through software for my load and grain weight is great, but again, you have to know the set up well and recognize its limitations before you really put too much faith into it.
Thanks for your review. I have seen some others that have come to similar conclusions. I bought one of these in .308 on Black Friday. After the $100, mine was only $299. For that price for a heavy barrel .308, I had to be all over that.
Was first in line, filled out the 4473 form, but the NICS check was so swamped, it shut down. Had to return the following morning, and paid for it then.
Haven’t shot it yet, and ammo is getting very scarce. I am looking forward to going to the range, though.
Almost exactly 2 years ago I was shopping for my first “deer rifle” and had a $100 gift card for Sports Authority. I walked out with a 700 ADL in 30-06 with a stainless steel action and barrel.
I had the same experience with the scope/scope rings being crappy, but the rest of the gun being otherwise pretty nice. I have since upgraded the scope to a Leupold VX2, and I have installed the Remington spacer kit (I’m 6ft2, so I tend to like a longer LOP).
I have to admit that I’m still not getting the groupings that I would like, but I think it has more to do with me (I have to work hard not to flinch or possibly using CMP mil-surp 30-06.
You mention flinching, which is telling me that you are having problems caused by the recoil of the weapon. I don’t think a .30-06 is a good “beginner’s” gun, because the recoil is noticeable (not as compared to a .458 Lott or .375 H&H, but still). I know lots of guys swear by it for deer, but I think it is overkill, esp. blacktails and whitetails. I think its better to very accurate and hit vitals rather than using brute force to compensate for poor shot placement. If you can’t shoot an apple sized target at 200 yards then you really can’t shoot well, IMHO. For deer, I really prefer milder rounds like the .30-30, .357 Magnum, .243 Win, 7mm.08, 7x 57, .257 Ackerly, etc. If you actually can hit a vital, a 95 grain .243 Win is more than enough bullet to quickly put a deer down.
Recently set up a female friend of mine with a Stevens (Savage) Model 200 in .25-06 that bought off a friend for $200 and change. It was fairly mild shooting rifle and also very accurate (Most groups were in the 1/2 MOA range, but I shot a 1/4 inch group at 100 yards with that rifle). She killed a deer with it on her first hunting trip.
A muzzle brake will tame the recoil of the 30.06, but most brakes have the downside of increasing noise levels significantly. Also, get some snap caps, and practice dry-firing the rifle. Have a friend balance a penny on the barrel (near the muzzle) and work on dry firing the rifle without tipping the penny off of the rifle.
I have a couple thousands rounds of the CMP .30-06 – the stuff I got was de-linked machinegun ammo. Its not the most accurate stuff in the world by a long shot, but it is fairly low powered so it won’t beat the hell of a Garand’s op-rod like commercial ammo will do. For your purposes, I would try a few boxes of Hornady, Black Hills, or Federal (their Fusion line is great ammo and fairly good priced for what you get), and see what that does to your groups sizes. Good luck.
You are correct, I started out with tons of recoil issues with the gun. The biggest one was that the cheap factory scope had such a short eye relief that 4 out of 5 shots would result in the scope hitting my safety glasses and cutting the bridge of my nose.
I upgraded the scope to the Leupold VX2 (much longer eye relief) and shot it some more (multiple trips to the range), but still didn’t get great groupings (still larger than 4″ at 100 yards).
After that, I attended the RWVA Appleseed camp twice and qualified as a Rifleman. I also installed the Remington stock extension so that the LOP was long enough I could actually use my right arm to pull the gun in. Having the correct LOP and using the lower power CMP ammo have both reduced the felt recoil, but my groupings haven’t improved.
I could still be flinching (I’ll have the fiance’ watch for that next time I go out), but I feel like I’ve reduced the recoil a noticeable bit, and I am doing everything I can to slowly squeeze the trigger and follow through with the shot. Also I can get good groupings out of other rifles in similar calibers. Maybe I still associate it with being a nose smasher?
I know this is something people usually do with handguns, but if you think flinching is still a real possibility, have you tried snap caps? They’re about $9 for a pair of ’em at Bass Pro.
Have someone else load your magazine (maybe even chamber a round — live or not — for 4+1 if you’re feeling froggy) without you looking. Have ’em put some random number of snap caps in with the live rounds (although I wouldn’t recommend zero because that would negate the exercise). Then when you pull the trigger, if it’s on a snap cap you’ll see real quick if you’re flinching.
One note: if you work the bolt at medium speed or slower, it’s really easy to tell when you’re chambering a snap cap versus a live round. They’re aluminum and have a machined finish on them, so you can feel them “zip” into the chamber. But I’ve found that if you’re not babying the bolt, it’s really hard to tell the difference.
Finally got the 700 out to the range yesterday. I discovered my problem is not so much flinching, as it is poor trigger discipline.
To elaborate, most of my other firearms have triggers that have a decent amount of take-up. In comparison, my 700 ADL has very little take-up. Turns out I have developed a bad habit of getting close to on target (within an inch or so)…squeezing out the take-up…getting on target… then following through with the shot. Not only is this process less than ideal for all firearms, but with the short take-up of the 700 ADL I sometimes find myself firing before I’m completely on the bullseye.
So now I have trigger discipline to work on through dry firing.
That ADL was a heckuva deal. It’s hard to say no to a quality piece like this, at such a bargain basement price tag. Several big-box stores carry ’em, like Walmart, so that’s a good place to catch ’em on sale as well. For $350, what’s not to like?
Hey, Thanks. That comment made my day! Well,…. that and shooting an Accuracy International AX 308 ! 🙂
I saw a video on 8541 tactical where he took the action from that same gun a put it in a chassis stock. he stated the action is the same action that is in the upper end 700s. from what I saw in the price of actions it was worth it to buy the gun just for the action and the heavy barrel. Im thinking of doinf the same for a .223, already have a .308 with a tactical/ varmint Bell & Carlson Stock
jim
Just got one of these in 308. Put on a Nikon 6-18×40BDC that I had laying around. Printed 3 holes touching at 100yds with Black Hills 168gr BTHP. Best group I ever shot. Needs a trigger as this one feels like 5 #’s. This is my 5th Remy 700 acquired over the years and they all shoot sub moa with match ammo.
There is a kit available to convert the ADL to a BDL.
http://www.brownells.com/rifle-parts/triggers-bottom-metals/adl-bdl-conversion-kits/remington-700-adl-to-bdl-kits-prod340.aspx
This is another reason that the ADL is worth it’s price all day long. You can start there, do the conversion later on and also replace the stock, and so on. The price difference is about $350 between ADL and BDL, that’s pretty much where you would be at after the conversion and a decent aftermarket stock.
That’s pretty damn cool, Nate. Thanks!
Going to pick up my first Remmy 700 ADL later today my local wallyworld stocks them in almost every cal I think I wil go with the 270 and for 417.88 its still not a bad price seeing as they dont charge for background check
I purchased a Remington 700 ADL Wood Tech in .308 this past fall. It was a scoped “combo” that came with a bushnell 3-9×40 banner on sale for 549.99. The only .308 ammo that I could find at the time was Hornady’s American Whitetail loaded with 150 gr. interlocks. the first thing I noticed was the action was surprising smooth. The second thing I noticed was the fine accuracy this rifle is capable of, 1/2 MOA 100 yd. groups easily obtained from the sporter pipe. The third thing I noticed was the last round in the magazine would not feed…ever. Its a common ADL issue. A different bullet may solve this problem, but I think a BDL or DM conversion is the best solution for any ADL rifle.
What’s .270 Rem? Is there a magical new .270 cartridge apart from the .270 Winchester?
Correction made!
I am sorry to say that the Reminton 700 Varmint that was advertised in todays paper for $499.00 with a $50.00 rebate is no longer available as it has been recalled by Remington because of a problem with the new trigger which can cause it to discharge without pulling the trigger, I mean really, our local store in Pleasant Hill, Ca. just had their Grand Opening today and the rifle is unavailable nor are they offering rain checks for when the trigger problem has been resolved, you can check this out on Remington’s Website!!
True, but fortunately, during that same week, Dick’s Sporting Goods *was* offering the Savage 11 VT 24″ Heavy Barrel (.223 and .308) for $449 as a substitute. Yep, AccuTrigger included. That, too, was quite a good deal.
All that’s left is to find out which one shoots better, the ADL or the 11 VT. Savage quality is well known by now, but given how well the ADL shoots, I’m not sure which one’s going to “win”. Either way, though, the customer really wins, because both Rem 700’s and Savage 10/110’s are good rifles.
– T
Thanks for your detailed review. As a gift I received the Remmy 700 SPS Stainless .308 from my lovely wife who participated in the Black Friday sale the year after you. The same scope came on it, and like you, not impressed. Due to my employment, the only opportunity I had to put rounds in this beautiful-affordable craftsmanship was one box while trying to zero the sights shortly after the new year. This year, I have told my wife that I want to upgrade the scope for my birthday (early november, right before gun season where I live). Though I hunt whitetail, I am considering going with the same scope you have for coyote hunting. I think it will work just fine.
Care to give any advice on that idea, or suggestions?
Thanks
Natchez Shooters Supply has really good deals on these Nikon scopes. Although I am generally a total optics snob, I think these scopes meet my needs. I was hitting steel at 600 yards with mine last weekend, and varmints don’t stand a chance.
I purchased this same rifle, Remington 700 ADL .308 26″ Varmint Mossy Oak, from Dicks on black Friday last year 2014. I’m curious of where you got the information on the barrel twist being 1:14 as the article states? I called Remington and gave my serial number and they told me mine was 1:12. Thanks
He was referring to a different caliber for his barrel twist.
Remington 700 SPS Varmint’s Trigger Guard is a piece of Garbage!
My gun is less than 3 months old. While cleaning it, I always drop the magazine.
The bottom plate’s neck latched into the trigger guard broke and fell to the ground.
Then I discovered, it was made of Cast Aluminum, Not Solid Aluminum. Maybe made in China! On top of this, Remington’s Customer Service Warranty Sucks! Boy it took 2 weeks and the order is still in process. So I called after two weeks then learned that the first rep who took my warranty claim put the wrong part in. So the 2nd rep I spoke to, just put a new order. Thus is will take another 2 weeks to process. Unbelievable Customer Service/Warranty Support. I was happy with the Gun until it broke under normal circumstances/use.
Remington! Get your act together! Stop using cheap made in China parts! Improve your Customer Service/Support!
Lastly, if you plan to continue using these cheap made in China parts, at Least Improve your Documentation to say, Please catch the cheap bottom plate at the Trigger Guard so the Cheap China Part will not Fall Apart! Love the Gun but not Remington’s Customer Support….. Now, I can go back to my normal life since I’ve released my disappointments and frustrations with Remington.
“PETA types routinely soil their diapers over any type of hunting, but their hysteria is completely illogical when you think about it. Coyotes typically end their lives in starvation, hypothermia, or the gnashing jaws of other predators”
This logic is analogous to justifying the execution of prisoners in a concentration camp because they would just die awful deaths anyway.
Typical gun writer; incapable of writing an objective, fact-based article about the mechanics and performance of the firearm without inevitably digressing on an irrelevant and angry personal or political diatribe. Nice going.
Thanks, very interesting review and a lot of useful information about Remington 700 ADL Varmint.
This was very classy and helpful. So I purchased one. Thanx for the info. Me thinks a Cabelas Vortex scope is the one yet partial to Nikon it’s true of the Coyote scopes and Bmasters. Have three Coyote scopes different variables and they work. Optics World does not offer a warranty nor Nikons ltd warranty protects you like Cabelas Vortex warranty.
That’s not a Cabelas warranty, it’s a Vortex warranty. I worked for Cabelas for a couple of years.
The Vortex warranty is outstanding. Another scope company to consider is Sig Optics of Oregon. I have 3, 1 in mounted on a .308 win; a .300 win mag; and a .340 Wby mag.
All are FFP and they can handle the recoil of both magnums. Something the Nikon couldn’t do on the .300 win mag (Browning X-bolt).
Nikon has an app, “Spot-on”. It’s basically a ballistic calculator for the BDC Nikon reticle and other nikon scopes. It covers an extremely large selection of calibers/rifle actions/bullet specs. Works well on Android, not so much on Appel.
Nikon needs to start offering their scopes with standard duplex. The BCD is costing them sales. They also need to redesign the power selector ring on the monarch’s. As is it is ugly.
Slim Fit Leather Jackets is an online store where we sell jackets for men and women with free shipping all over the world! Visit Our Site and Get Your Favorite Actors or Actresses Outfits now at the best prices.
Comments are closed.