I’ve been waiting for my NFA paperwork for my silencer since October. When I submitted the paperwork, everyone I talked to said the ATF would take 60 days to process my stuff and then I’d be the proud new owner of a tax stamp. I’m still waiting. And getting slightly annoyed. So I emailed Erich, the guy in charge of NFAtracker.com, and asked him to give me a dump of his database to figure some stuff out. He complied, and then I almost lost my mind.

First things first, a quick note on how NFA paperwork works and the methodology for the following graph.

As soon as you submit your paperwork to the ATF, they cash your check and then sit on it for a bit. The length of time they sit on it varies, but at some point you can call the ATF’s NFA branch hotline, provide your serial number and they will inform you that your paperwork is “pending.” That means that an examiner has been assigned to your stuff, and it is now being worked on. Eventually, if you have led a good life, your paperwork will move to “approved” and your stamp will be issued shortly.

The ATF doesn’t release statistics about wait times and things like that, so in order to figure out what’s going on in terms of wait times NFA paperwork applicants have taken to indirect observation through self reporting. NFAtracker.com is a website where applicants self report the time it’s taking them for their paperwork to process through the ATF, and in turn the site auto-computes some statistics so that those still waiting can have an idea of how long things are going to take. So while these results may not be completely accurate, they are derived from the only 2,458 records I could get my hands on.

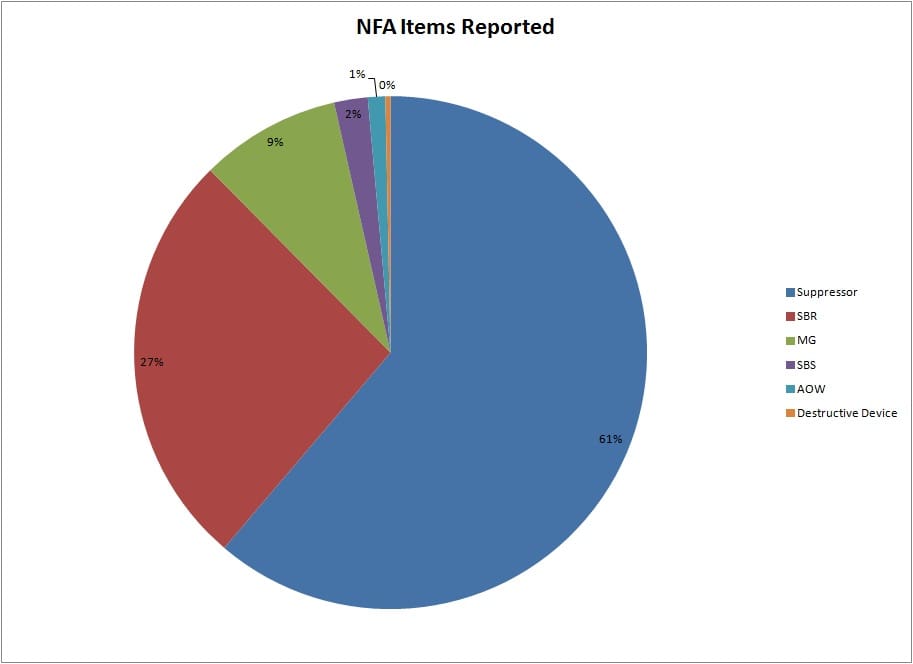I focused my efforts on silencers, since they constituted the largest proportion of the database (and for personal reasons), but I figured that the wait times for silencers would give an image of what the times are like for the other NFA items as well.

And that image is not very hopeful lately.

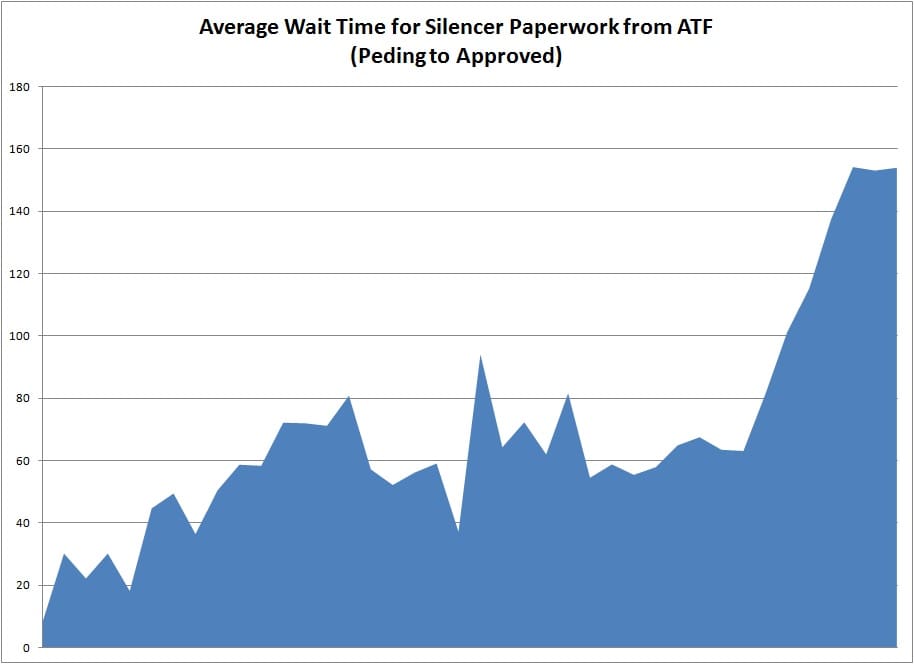This graph is the product of a night of pouring over the data dump from NFA tracker, slicing the data into 30 day windows based on when the paperwork was sent in and focusing solely on silencers. I examined how long it took for the paperwork to go from “pending” to “approved,” slicing out shipping time and most of the other factors that would influence how long it takes to get a tax stamp but be unique to a specific case. Last year the average wait was indeed somewhere around 60 days, but lately (the last 3-4 months) the wait time has exploded past 140+ days and stayed steady at that point ever since. Wait times have almost doubled.

Why? We can only speculate, but I have an idea.

The primary force behind this increase is probably that the volume of NFA items being processed is absolutely overwhelming the ATF. Which, considering the recent uptick in entries for NFA items in NFAtracker.com’s database, makes sense. Silencers have taken off in recent months, especially with the legalization of silent hunting in certain states and the ever-decreasing financial pain of that $200 stamp (thanks inflation!). And while the volume of paperwork has increased, the ATF has not (that we can tell) made any investment whatsoever in their NFA paperwork processing systems. It’s like trying to funnel all the traffic from I-95 down your town’s main street — it just can’t handle that type of volume.

The solution is obvious: hire more NFA paperwork people or modernize the process. But given the ATF’s priorities I get the feeling that it will be a while before any of their budget is available to make things easier for law abiding gun owners rather than harder.

Back in Fairfax, Virginia, the local law states that an applicant for a concealed carry license can be kept waiting no longer than 45 days for their permit. Even though the paperwork only takes a couple of hours to complete, the county sheriff will purposely wait until day #43 to mail it to you. Why? Because making things inconvenient for the law abiding public seems to be a way of life for some government officials.

Just like Fairfax County, I get the feeling that the ATF is rejoicing in the increased pain and suffering of law abiding gun owners. But I pray that I’m proven wrong and they actually ramp up their NFA branch to deal with the flood of paperwork.

RELATED ARTICLESMORE FROM AUTHOR

64 COMMENTS

  1. The answer is to move to a state with the Firearms Freedom Act and learn how to operate a lathe and mill if you want suppressors 😀

    • While you’re at it you may also want to acquire or perfect some other skills like: sleeping with one eye open
      filing a spoon into a shank
      power gripping soap in the shower

      • Some of the states that have adopted this actually have felony level penalties for anyone enforcing the federal NFA. It is definitely a fight between state’s rights and the overstepped federal mandates.

        Although I wouldn’t want to be a test case, there are quite a few people taking advantage of this new legislation; they just don’t broadcast it.

        • The states have made their laws, let them enforce them, especially when highway money is on the line.

  3. Nick, what’s the abscissa on graph 2 please? You appear to have the wait time in days as the ordinate, but what are you plotting against on the x-coordinate?

    • 30-day increments based on when the forms were submitted. It’s not exactly lining up with the months, so I decided against putting notes on that axis.

  4. A better solution would be to get suppressers off of the NFA, or repeal the freaking NFA.

    The only argument we should need is “Many European countries sell them like candy bars at hardware stores”. We can’t allow ourselves to be out firearm freedomed by the sissy nannies across the pond

    • You know, that’s really not a bad idea! After all, the libs seem overly impressed by just about anything else “european”, to the point of wanting to pass laws to make us more like the EU and decide court cases based on their laws rather than ours… Why not push for copying their “enlightened” attitudes about suppressors? Would be really interesting to see Ginsburg’s take on it…

    • I resemble that remark!!! 🙂

      All we need to do here in the UK is show good reason for having a suppressor (or sound moderator as we prefer….) & this is covered by stating a reduction in noise pollution & protecting the shooter’s & others’ hearing.
      If I want one for an air rifle then I don’t need anything; just walk in & buy one. Many of these are exactly the same quality as those for .22RF – only they don’t have a proof mark.

  5. I am not surprised by this though I am surprised that your people in the know says this takes 60 days. This will take you 6 months at minimal, real life experience dealing with it multiple times in the last two years.

    • I have a friend who has literally been in the pipeline for close to a year, but that was due to the form not being double sided (d’oh).

      • States are free to craft their own rules (and to completely outlaw NFA firearms if they so choose). The state’s rule making power extends to NFA trusts. So, state laws must always be reviewed carefully, since there is no end to their mischief.

      • Actually, the correct answer is that it SHOULD be faster. That doesn’t mean that it will be.

      • I was going to get a Firearms Trust, and submit my application that way, but my attorney said:
        — I was just as legal doing it by myself, and appeared more “compliant” to the NFA Branch by doing it as “me”;
        — I was less likely to have it taken away from me if GA ever changed their trust laws, because personal property laws are almost never changed, but trust laws are often changed, and if they are I may end up fighting for position/ownership of my item with other members of the trust; and
        — It was easier to discern “ownership”, in case my item was ever lost or stolen. All a private owner would have to do is show an ID card to get an item back, as opposed to having to prove he was a member of the trust, and even showing proof that the trust owned the item.
        I got 2 stamps in about 4 months with no hassles from my Sheriff at all. All my Sheriff did was ask the dispatcher if I had any “stupid calls” at my house, and when she said “no”, he signed it right away, and said, “have fun!”.

  7. The Gemtech rep at the SHOT show warned me that the wait time for January applications would probably be 180 days or more.

  8. I just got my paperwork back on an AAC silencer. Just past 180 days. My fourth. The system is broken

  9. So criminals have to wait 180 days to get their hands on a silencer? Wow what a great law, this is government at it’s finest. No law breaking thug would ever want to break that law.
    How about some stats on how many crimes were actually committed with a suppressed weapon?

  10. As someone who is in the “shopping phase” for my first suppressor, this post makes me very, very sad.

    • GEEPERS!!!! Don’t be posting stuff like that! The BATF will be increasing the fee to $3500 just for shits and giggles. We ESPECIALLY don’t want certain antigun members of congress to see that as they would increase the fee in a heart beat to “increase revenue”.

        • If you read the debate surrounding the law, it was INTENDED to put such a burden on those who currently possessed an NFA item, that they would be afraid to sell it cheap to some gangster, and then forget to whom they sold it. At the time, gangsters were literally going door-to-door, asking folks if they had Tommy guns or Silencers from their WWI days. Congress caught wind of that, and NFA1934 was dreamed up by them and the many big-city citizens’ crime commissions.

          And, because some in Congress felt that they had “no authority to regulate guns in use by the Militia” (yeah, it surprised me to read some Congressman say that, too!), they only regulated the TRANSFER of certain guns from one owner to another.

          Maybe, one day, Congress will RETURN to the belief some of them had back in the 30s (that they have no right to ban certain firearms because it harmed the Militia by doing so), and we’ll get back to the freedoms this Nation enjoyed PRIOR to the 1930s.

  12. If the ATF was actually dragging its feet on approvals, the wait would be years, not months. I have no inside source, but my guess is that staff has decreased while demand has increased.

  13. I’ve been waiting for my supressor stamp (SS Sparrow) since Nov 2nd, and a SBR stamp since Feb 3rd.

  14. ATF had a hiring freeze placed in 2011 by Holder, so combined with Silencerco and AAC’s advertising campaigns and several states legalizing suppressors for hunting use, the industry got a large increase in suppressor applications combined with no new ATF 5320 inspectors.

    http://abcnews.go.com/Politics/justice-department-attorney-general-eric-holder-orders-hiring/story?id=12749770#.T0_Y-4ePXSg

    This is less a case of government obfuscation and more a case of bad timing.

  15. “Of the federal court cases reported in
    the Lexis/Westlaw database between 1995 and 2005, there
    are only two cases of a silencer being used in a murder in
    the United States.”

    this was out of a research paper. All other cases were deemed victimless(possesion charge).

    52% of the 156 cases involving suppressors in those 10 years were .22 suppressors, and no details were given if any were homemade or not. so all that time and money to catch 15 guys a year with only 136 convictions and 7 plea deals

    • And, our own Assistant US Attorney refused to prosecute a guy just last year, because he felt he “had no jurisdiction” in the case of a convicted felon with a gun. And, the gun the convicted felon had? A sawed-off shotgun. Crime statistics are manipulated by agencies all the time, in an effort to show good conviction rates, keep politicians from being exposed as lazy, and to get more money for struggling agencies. Don’t forget, there are “lies”, “damned lies”, and “statistics”… …and, ALL OF THEM are lies.

  16. “The solution is obvious: hire more NFA paperwork people or modernize the process.”

    That’s a stop-gap measure. The solution is to repeal the NFA.

  17. YOUR tax dollars hard at work!!!
    These people work for us and they think they are the boss.
    And the Federal Government is at least 14 Trillion dollars in debt?
    Is that all?

  18. I’m willing to bet that NFA taxes are one of the only things profitable in the federal government (though unreasonable in its enforcement).

  19. This should be something the NRA’s ILA group should be working on. They should get some friendly Senators and Congressmen to start asking the ATF why things are taking so long and offering to introduce legislation to repeal or modify the NFA to “help” the ATF if they are getting overwhelmed.

    • The NRA doesn’t care about NFA issues! All they care about is making themselves look “innocent”, while making other pro-gun groups look like they should to be on the Terrorist Group Watch List. The NRA can show Heston saying on video, “…from my cold, dead hands!”, all they want, just know this: the NRA will give up their membership roster QUICK to the feds, if they are ever asked for it! Don’t waste your money with them any more. Join a REAL pro-gun group that is concerned about FIREARMS FREEDOM, not just some hunter’s right to use a semi-auto shotgun with buckshot on federal land.

  20. All the ATF folks are probably busy shredding paperwork related to fast and furious, so they have no time to process NFA paperwork!

  21. http://blog.princelaw.com/2012/01/20/shot-show-2012-atf-town-hall-meeting-and-nfatca-meeting-dealers-and-manufacturers-take-notice/
    “The issue of ATF Form 1 and Form 4 processing was also brought up. ATF’s response was that they are under the hiring freeze of the DOJ and while they have attempted to bring in temporary employees and move people around from different departments, due to the increase in NFA applications, the wait time of 4 – 6 months is not likely to change anytime soon.”

  22. The solution is obvious … congress should exempt suppressors and SBRs from the purview of the NFA.

  24. Typical government insanity, criminalize everyone because there is a tiny minority that may hurt someone. Um, criminals don’t care about stamps. Or laws.

  25. How many drive-by MAC-10s and Tec-9s have NFA stamps? If the answer is less than “most of them” (and we all know that is the case, since no NFA item has ever been used in the commission of a crime), the NFA accomplishes nothing.

    Except to pad the .gov’s pocketbook. The BATFE is part of the Treasurry, after all…

    • Actually, NFA items which have been STOLEN have OFTEN been used in crimes. And, without items being registered by NFA, the BATFE would have no idea to whom to return the item, once it HAS been found.

  26. I had a problem waiting, too, but my 2 stamps finally came back to me (together in the same envelope), after about 4 months. I’m a retired Federal LEO, so it was probably easier to do my background check, but I was told by NFA Branch when I called them that they do background checks based on a person’s “place in line”, and not by “who they are”, so my being a retiree didn’t matter much to them.
    Since I have a buddy who works at BATFE, I asked him if he had any idea why it took so long for an NFA background check, when they normally don’t take more than 30 days for every other branch. He said that the NFA Branch only has 8 or 9 agents, and these agents are the only ones authorized by law to do background checks the 350+ NFA applications they recieve each month. So, perhaps it might be better if a law was passed to allow TECHNICIANS to perform these background checks, and the agents to only approvh the stamp. That’s the way the government does it with employee applications at the Office of Personnel Management, a “technician” or “contract agent” gets all the background together, and a special agent only rubber-stamps the background for a person to be hired.
    It is obvious those 8 or 9 agents are over-worked, but they cannot bring in agents from other branches right now, because of all the OTHER b.s. Congress has them doing. I don’t think it’s going to get any better soon, either. And, darnit! I was hoping to add one more NFA Stamp to my “stamp collection”, too.

  27. So you mean to tell me that there are approximately 350 applications / month at the NFA Branch? To be split among 8 or 9 agents?

    Let’s think about this. Let’s say there are 450 applications per month. Divide 450/30 days per month. That’s 15 per day. That’s 15 apps / 8 agents is 1.875 or 2 (TWO) applications per agent, per day. Consider what has to be done here. They have to send off fingerprints to the FBI, double check the CLEO signature, and part of the day they should be spending approving transfers that they have already sent and gotten back from the FBI. In an 8 hour day, they should EASILY be able to process 2 or (GASP) THREE applications per day.

    From my experience, they are as usual, stumbling backwards to collect their paycheck… with only a couple of notable exceptions.

    My $200 worth… and I’ve been doing this for nearly 30 years.

    • I don’t think you realize just what’s involved in a “background check” here. You have to look at the person himself, see whether he’s telling the truth about his home address, telephone number, and ID information (all of which have to be independently verified by other, sometimes local and state agencies and databases), and then you start going through his fingerprint card (which inviles the FBI fingerprint database and all of it’s hassles, “red flags”, and “false flags” and “false posititives”, etc.), then you check his name against the federal criminal warrants list, all and 50 state warrants lists, then his name against the Bureau of Prison’s inmate registry, then the US Courts list of convicted felons and pending felon cases, etc. That’s a LOT of “paperwork” for one person to do in 1 day. So, could you REALLY do 3 per day? Come on, man. I’ve personally seen JUST ONE background check on a KNOWN FELON (an incarcerated inmate) take up-to 15 days for his hard file to come from Atlanta via FedEx, his pending charges to take up-to 10 days to come from Washington DC via FedEx, and his local prison file to come from his Unit Team (counselor, case manager, and unit manager) in up-to 5 days, and his unit team is usually less than 100 yars away from the admin building. I’m guessing these “8 or 9 agents” ARE over-worked, but there’s no pleasing some people. Yes, we KNOW there are problems with the system, but a federal law that requires a “special agent” to be the ONLY ONE to do a background check is a little silly, IMHO. Let a “technician” do the ground-work, and the agent can do the “approval”, and there will be less time between submission and approval, I assure you. But, who am I, just someone who’s been PART OF “the broken system”, and knows it takes “time” to figure out whether someone is a criminal or not. And, we’re not even GOING to assume what he PLANS for his NFA item, because ass-u-ming that violates his right to have it. All I’m saing is I can see how those guys at NFA are swamped. And, I don’t see it getting any better/faster, because CONGRESS is in the way, not the BATFE. Good luck to you, either way!

  28. You bring up very valid points, many of which I agree. It’s just been my experience that most of these agents don’t know the rules very well and they DO back up to collect their paychecks. There have been times where some of them have shredded paperwork and claimed them as “LOST” so they don’t have to do the work. They make a mistake, and we pay – sometimes becoming a felon because of their mistake! And yes, I do understand that there are other things they must do. They just need to streamline the system… Good reply, though.

  29. Gentlemen…..It’s all about taxation, certainly not about who’s the bad guy….after all most bad guys are broke!

  30. I spoke to a gentleman in TX. who has been selling suppressors for years. He told me that the ATF has only 9 people to process these forms and the rate of applications has gone through the roof. I have searched on many sites shopping for suppressors and have found that there are apparently many models out of stock now. This would seem to me to verify the upsurge in applications as well as illustrate to some degree the disparity between applicants and agents who are actually involved in the approval process. Just my two cents worth.

  31. Just had one of my Form 4’s approved June 9th, went pending Jan. 9th. It would appear to be leveling off to right at 5.5 to 6 month wait once your form goes pending. If you look at my approval date looks like they are trying to speed things up, (it was a Saturday) because I’m not aware of many Federal or even State employees that work weekends 🙂

  34. What I don’t understand re this “Wait time” is….WTF are they checking for? You purchase a firearm and a background check takes minutes. A silencer which is an attachment to a fiream and does NOT have the ability to harm anyone unless you throw it and hit someone in the head.

    With that being said and in my case (s) only, this is the second silencer I have purchased within months of the first, All of the preliminary investigation has already been done and a check for recent violations or what ever it is they are looking for should only take a stroke of a computer keyboard.

    In short…..Why does it take longer for a silencer than a firearm? Inquisitive and competent minds wonder!

Comments are closed.